题目内容
已知∠α为锐角，且tan（α+β）=3，tan（α-β）=2，则∠α= ．
考点：两角和与差的正切函数
专题：三角函数的求值
分析：利用两角和的正切求出tan2α，结合角的范围得答案．
解答：
解：tan2α=tan[（α+β）+（α-β）]=
=
=-1．
∵∠α为锐角，
∴0°＜α＜90°，0°＜2α＜180°，
∴2α=135°，
则α=67.5°．
故答案为：67.5°．
| tan(α+β)+tan(α-β) |
| 1-tan(α+β)tan(α-β) |
| 3+2 |
| 1-3×2 |
∵∠α为锐角，
∴0°＜α＜90°，0°＜2α＜180°，
∴2α=135°，
则α=67.5°．
故答案为：67.5°．
点评：本题考查了两角和的正切公式，是基础的计算题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
设数列{an}，a1=1，前n项和为Sn，若Sn+1=3Sn（n∈N*），则数列{an}的第5项是（ ）
| A、81 | ||
B、
| ||
| C、54 | ||
| D、162 |
已知命题p：?x∈R，tanx＜1，则（ ）
| A、￢p：?x∈R，tanx＞1 |
| B、￢p：?x∈R，tanx≥1 |
| C、￢p：?x∈R，tanx＞1 |
| D、￢p：?x∈R，tanx≥1 |
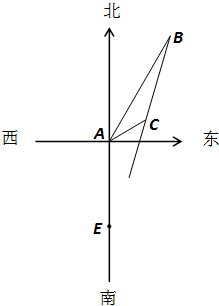在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域．点E正北55海里处有一个雷达观测站A．某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40