题目内容
14.甲、乙、丙 3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法总数是( )| A. | 210 | B. | 84 | C. | 343 | D. | 336 |
分析 由题意知本题需要分组解决,共有两种情况,对于7个台阶上每一个只站一人,若有一个台阶有2人另一个是1人,根据分类计数原理得到结果.
解答 解:由题意知本题需要分组解决,因为对于7个台阶上每一个只站一人有$A_7^3$种;
若有一个台阶有2人另一个是1人共有$C_3^1A_7^2$种,
所以根据分类计数原理知共有不同的站法种数是$A_7^3+C_3^1A_7^2=336$种.
故选:D.
点评 分类要做到不重不漏,分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.分步要做到步骤完整,完成了所有步骤,恰好完成任务.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列说法中正确的是( )
| A. | 命题“p∧q”为假命题,则p,q均为假命题 | |
| B. | 命题“?x∈(0,+∞),2x>1”的否定是“?x°∈(0,+∞),2x°≤1” | |
| C. | 命题“若a>b,则a2>b2”的逆否命题是“若a2<b2,则a<b” | |
| D. | 设x∈R,则“x>$\frac{1}{2}$”是“2x2+x-1>0”的必要而不充分条件 |
2.已知集合A={x|(x-2)(x+1)≤0,x∈R},B={x|lg(x+1)<1,x∈Z},则A∩B=( )
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
9.已知x,y满足$\left\{\begin{array}{l}{x-1≤0}\\{y-2≤0}\\{2x+y-2>0}\end{array}\right.$若$\overrightarrow{m}$=(x+1,y)则$\sqrt{{\overrightarrow{m}}^{2}}$的取值范围为( )
| A. | (15,2) | B. | ($\frac{29}{2}$,2$\sqrt{2}$) | C. | (17,2$\sqrt{2}$) | D. | ($\frac{4\sqrt{5}}{5}$,2$\sqrt{2}$] |
19.“log2(2x-3)<1”是“$x>\frac{3}{2}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.已知x、y都是非负实数,且x+y=2,则$\frac{8}{(x+2)(y+4)}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
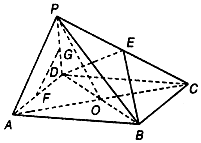 如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC、BD相交于点O,点E、F、G分别为PC、AD、PD的中点,OP=OA,PA⊥PD.
如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC、BD相交于点O,点E、F、G分别为PC、AD、PD的中点,OP=OA,PA⊥PD.