题目内容
18.(1)如果角a的终边在第二象限.讨论$\frac{a}{2}$的终边所在的位置.(2)由此可否得出更一般的结论?并画出a的终边在第一、二、三、四象限时.$\frac{a}{2}$的终边所在的位置.
(3)类似地讨论$\frac{a}{3}$的位置(可设a在第一象限.讨论$\frac{a}{3}$终边的位置.井推广到一般情形).
分析 (1)写出第二象限角的范围,可得$\frac{a}{2}$的终边所在的位置;
(2)直接由(1)的结论推广得到a的终边在第一、二、三、四象限时,$\frac{a}{2}$的终边所在的位置,并画出图形;
(3)由a在第一象限,讨论得到$\frac{a}{3}$终边的位置并进一步推广到一般情形.
解答 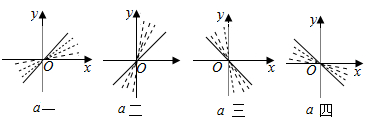 解:(1)由角a的终边在第二象限,得$\frac{π}{2}+2kπ<a<π+2kπ,k∈Z$,
解:(1)由角a的终边在第二象限,得$\frac{π}{2}+2kπ<a<π+2kπ,k∈Z$,
则$\frac{π}{4}+kπ<\frac{a}{2}<\frac{π}{2}+kπ,k∈Z$,
当k为奇数时,$\frac{a}{2}$的终边在第三象限,当k为偶数时,$\frac{a}{2}$的终边在第一象限;
(2)由(1)可得,当a的终边在第一、二、三、四象限时,
$\frac{a}{2}$的终边分别在第一或第三、第一或第三、第二或第四、第二第四象限;
如图:
(3)当a的终边在第一象限时,即$2kπ<a<\frac{π}{2}+2kπ$,得$\frac{2}{3}kπ<\frac{a}{3}<\frac{π}{6}+\frac{2kπ}{3},k∈Z$,
∴$\frac{a}{3}$的终边在第一或第二或第三象限;
推广可知:当a的终边在第二象限时,$\frac{a}{3}$的终边在第一或第二或第四象限;
当a的终边在第三象限时,$\frac{a}{3}$的终边在第一或第三或第四象限;
当a的终边在第四象限时,$\frac{a}{3}$的终边在第二或第三或第四象限.
点评 本题考查象限角和轴线角,考查集合思想方法的应用,是中档题.

练习册系列答案
相关题目
8.在等差数列{an}中,a1+a5+a9=12,则它的前9项和S9等于( )
| A. | 9 | B. | 18 | C. | 36 | D. | 72 |
9.直线$\sqrt{3}$x-y+1=0的倾斜角的大小为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
6.在直角坐标系xOy平面上,平行直线x=m(m=0,1,2,3,4),与平行直线y=n(n=0,1,2,3,4)组成的图形中,矩形共有( )
| A. | 25个 | B. | 100个 | C. | 36个 | D. | 200个 |