题目内容
12.在△ABC中,a,b,c分别为A,B,C的对边,已知a,b,c成等比数列,a2-c2=ac+bc,a=6,则 $\frac{b}{sinB}$=( )| A. | 12 | B. | $6\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 6 |
分析 a,b,c成等比数列,可得b2=ac.已知a2-c2=ac+bc,可得b2+c2-a2=-bc,利用余弦定理可得A,再利用正弦定理即可得出 $\frac{b}{sinB}$的值.
解答 解:∵a,b,c成等比数列,
∴b2=ac.
在△ABC中,∵a2-c2=ac+bc,
∴a2-c2=b2+bc,即b2+c2-a2=-bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=-$\frac{1}{2}$,
∵A∈(0,π),
∴A=$\frac{2π}{3}$.
∴由正弦定理:$\frac{b}{sinB}=\frac{a}{sinA}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$,
故选:C.
点评 本题考查了正弦定理、余弦定理、等比数列的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
4.在数列{an}中,a1=1,$({n^2}+2n)({a_{n+1}}-{a_n})=1(n∈{N^*})$,则通项公式an=$\frac{7}{4}-\frac{2n+1}{2n(n+1)}$.
1.已知直线l:xcosθ+ysinθ+2=0与圆x2+y2=4,则直线l与圆的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 与θ的取值有关 |
2.如图,网格上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的表面积为( )
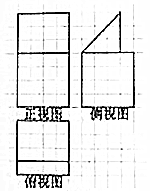

| A. | 93+12$\sqrt{2}$ | B. | 97+12$\sqrt{2}$ | C. | 105+12$\sqrt{2}$ | D. | 109+12$\sqrt{2}$ |