题目内容
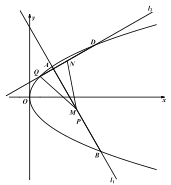
【题目】已知抛物线![]() 的图象经过点
的图象经过点![]() .
.
(1)求抛物线![]() 的方程和焦点坐标;
的方程和焦点坐标;
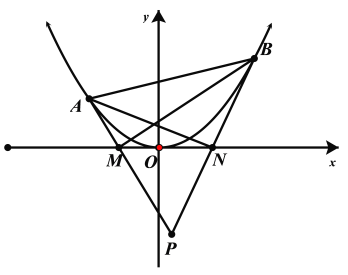
(2)直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 不同两点,且
不同两点,且![]() ,
,![]() 位于
位于![]() 轴两侧,过点
轴两侧,过点![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的两条切线交于点
的两条切线交于点![]() ,直线
,直线![]() ,
,![]() 与
与![]() 轴的交点分别记作
轴的交点分别记作![]() ,
,![]() .记
.记![]() 的面积为
的面积为![]() ,
,![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,试问
,试问![]() 是否为定值,若是,请求出该定值;若不是,请说明理由.
是否为定值,若是,请求出该定值;若不是,请说明理由.
【答案】(1)![]() ,焦点坐标为
,焦点坐标为![]() ;(2)
;(2)![]() 为定值且定值为1.
为定值且定值为1.
【解析】
(1)将点代入抛物线方程求出![]() 后可得所求的抛物线方程及焦点坐标.
后可得所求的抛物线方程及焦点坐标.
(2) 设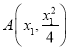 ,
,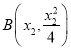 ,利用导数求出切线的斜率后可求切线
,利用导数求出切线的斜率后可求切线![]() 的方程,求出
的方程,求出![]() 的坐标后可用
的坐标后可用![]() 表示
表示![]() ,化简后可得
,化简后可得![]() 为定值.
为定值.
(1)将![]() 代入方程有
代入方程有![]() ,故
,故![]() ,所以抛物线的方程为
,所以抛物线的方程为![]() ,
,
焦点坐标为![]() .
.
(2)设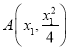 ,
,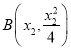 ,
,![]() 的中点为
的中点为![]() .
.
因为抛物线的方程为![]() ,故
,故![]() ,所以
,所以![]() ,
,
故直线![]() ,同理
,同理![]() .
.
令![]() ,则
,则![]() .
.
由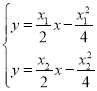 解得
解得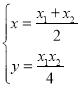 ,故
,故![]() .
.
因为![]() ,故
,故![]() 轴,又
轴,又![]() ,
,
所以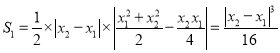 .
.
又![]() ,故
,故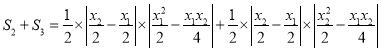
![]() ,
,
因为![]() ,
,![]() 位于
位于![]() 轴两侧,故
轴两侧,故![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() 为定值且定值为1.
为定值且定值为1.

练习册系列答案
相关题目