题目内容
10.已知数列{an}的前n项和为Sn,且${S_n}=2{a_n}-2(n∈{N^*})$.(1)求数列{an}的通项an.
(2)设cn=(n+1)an,求数列{cn}的前n项和Tn.
分析 (1)利用数列的递推关系式通过Sn-Sn-1=an,推出数列的等比数列,然后求解通项公式.
(2)利用错位相减法求解数列的和即可.
解答 解:(1)∵${S_n}=2{a_n}-2,{S_{n-1}}=2{a_{n-1}}-2(n≥2,n∈{N^*})$两式相减得Sn-Sn-1=2an-2an-1
∴an=2an-1,∴$\frac{a_n}{{{a_{n-1}}}}=2(n≥2,n∈{N^*})$即数列{an}是等比数列.
∴${a_n}=2•{2^{n-1}}={2^n}(n≥2,n∈{N^*})$,
∵${a_1}={S_1}∴{a_n}={2^n}(n≥1,n∈{N^*})$.
(2)∵${c_n}=(n+1){2^n}$${T_n}=2×{2^1}+3×{2^2}+4×{2^3}+…+n×{2^{n-1}}+(n+1)×{2^n}$…①…(7分)$2{T_n}=2×{2^2}+3×{2^3}+4×{2^4}+…n×{2^n}+(n+1)×{2^{n+1}}$…②…(8分)
①-②得$-{T_n}=4+{2^2}+{2^3}+{2^4}+…+{2^n}-(n+1)×{2^{n+1}}$
=$2+[{\frac{{2(1-{2^n})}}{1-2}}]-(n+1)×{2^{(n+1)}}$…(10分)
=2n+1-(n+1)×2n+1=-n•2n+1…(11分)
∴${T_n}=n•{2^{n+1}}$…(12分)
点评 本题考查数列的递推关系式以及数列求和,考查计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
20.下列说法正确的是( )
| A. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| B. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” | |
| C. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有$\frac{1}{{x}^{2}}$<$\frac{1}{{x}^{3}}$,则p∧(¬q)是真命题 | |
| D. | 从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分层抽样 |
1.已知函数f(x)=sin2x,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移$\frac{\sqrt{3}}{2}$个单位移,得到函数g(x)的图象,则当x∈[0,$\frac{π}{2}$]时,函数g(x)的值域为( )
| A. | [-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$] | B. | [-$\frac{\sqrt{3}}{2}$,1] | C. | [0,1+$\frac{\sqrt{3}}{2}$] | D. | [0,$\sqrt{3}$] |
5.已知a,b为实数,则“a5<b5”是“2a<2b”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |

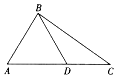 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且sinAsinAcosC+sinCsinAcosA=$\frac{1}{3}$sinC,D为AC边上一点.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且sinAsinAcosC+sinCsinAcosA=$\frac{1}{3}$sinC,D为AC边上一点.