题目内容
在△ABC中,|
|=3,|
|=2,点D满足2
=3
,∠BAC=60°,则
•
=( )
| AB |
| AC |
| BD |
| DC |
| AD |
| BC |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据向量的数量积的运算以及向量的几何意义,即可求出.
解答:
解:∵|
|=3,|
|=2,∠BAC=60°,
∴
•
=|
|•|
|cos60°=3×2×
=3,
∵2
=3
,
∴
=
∴
•
=(
+
)
=(
+
)
=
(
-
+
(
-
)2,
=
•
-|
|2+
(|
|2+|
|2-2
•
)
=3-9+
(9+4-6)
=-
故选:C
| AB |
| AC |
∴
| AB |
| AC |
| AB |
| AC |
| 1 |
| 2 |
∵2
| BD |
| DC |
∴
| BD |
| 3 |
| 5 |
| BC |
∴
| AD |
| BC |
| AB |
| BD |
| BC |
=(
| AB |
| 3 |
| 5 |
| BC |
| BC |
=
| AB |
| AC |
| AB) |
| 3 |
| 5 |
| AC |
| AB |
=
| AB |
| AC |
| AB |
| 3 |
| 5 |
| AB |
| AC |
| AB |
| AC |
=3-9+
| 3 |
| 5 |
=-
| 9 |
| 5 |
故选:C
点评:本题考查了向量的数量积的运算以及向量的几何意义,属于中档题

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
已知曲线C1的参数方程为
(θ为参数),曲线C2的极坐标方程为ρ=2cosθ+6sinθ,问曲线C1,C2是否相交,若相交请求出公共弦的方程,若不相交,请说明理由.
|
在Rt△ABC中,CA=CB=3,M,N是斜边AB上的两个动点,且MN=
,则
•
的取值范围为( )
| 2 |
| CM |
| CN |
| A、[3,6] | ||
| B、[4,6] | ||
C、[2,
| ||
| D、[2,4] |
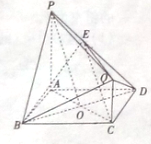 如图,直线PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC与BD相交于点O,E在线段PD上且CE∥平面PBQ
如图,直线PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC与BD相交于点O,E在线段PD上且CE∥平面PBQ