题目内容
如图,E是以AB为直径的半圆上异于A,B的一点,四边形ABCD是矩形,且AB=2AD=2,沿AB翻折,使平面ABCD⊥平面ABE,F为平面ECD与半圆弧的另一交点.
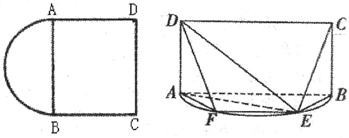
(1)求证:平面ADE⊥平面BEC:
(2)求证:EF∥CD.
(3)若EF=1,求三棱锥E-ADF的体积.

(1)求证:平面ADE⊥平面BEC:
(2)求证:EF∥CD.
(3)若EF=1,求三棱锥E-ADF的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)利用平面ABCD⊥平面ABE,CB⊥AB,证明CB⊥平面ABE,再根据直径所对的圆周角为直角,得到BE⊥AE.结合线面垂直的判定定理,得到AE⊥平面BEC,最后利用面面垂直的判定定理,得到平面ADE⊥平面BCE;
(2)先证明CD∥平面ABE,再利用线面平行的性质,即可证得结论;
(3)求出点E到直线AB的距离为3,转换底面,即可求三棱锥E-ADF的体积.
(2)先证明CD∥平面ABE,再利用线面平行的性质,即可证得结论;
(3)求出点E到直线AB的距离为3,转换底面,即可求三棱锥E-ADF的体积.
解答:
(1)证明:∵平面ABCD⊥平面ABE,CB⊥AB,平面ABCD∩平面ABE=AB,
∴CB⊥平面ABE,
∴CB⊥AE,
∵BE⊥AE,CB∩BE=B,
∴AE⊥平面BEC,
∵AE?平面ADE,
∴平面ADE⊥平面BEC;
(2)证明:∵CD∥AB,AB?平面ABE,CD?平面ABE,
∴CD∥平面ABE,
∵平面CDE∩平面ABEF=EF,EF?平面ABE,
∴CD∥EF;
(3)∵AB∥EF,AB=2,EF=1
∴点E到直线AB的距离为3,
∴VE-ADF=VD-AEF=
S△AEF•AD=
∴CB⊥平面ABE,
∴CB⊥AE,
∵BE⊥AE,CB∩BE=B,
∴AE⊥平面BEC,
∵AE?平面ADE,
∴平面ADE⊥平面BEC;
(2)证明:∵CD∥AB,AB?平面ABE,CD?平面ABE,
∴CD∥平面ABE,
∵平面CDE∩平面ABEF=EF,EF?平面ABE,
∴CD∥EF;
(3)∵AB∥EF,AB=2,EF=1
∴点E到直线AB的距离为3,
∴VE-ADF=VD-AEF=
| 1 |
| 3 |
| ||
| 12 |
点评:本题考查面面垂直的性质,线面垂直的判定与性质,考查线面垂直,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

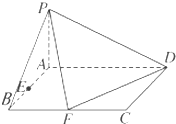 已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD,AD=2,AB=1,E、F分别是线段AB,BC的中点,
已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD,AD=2,AB=1,E、F分别是线段AB,BC的中点, 如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.