题目内容

19．如图所示，正方体ABCD-A1B1C1D1中，P、Q分别是AD1、BD上的点，且AP=BQ，求证：PQ∥平面DCC1D1．

分析 过P作PM∥AD交D1D于M，过Q作QN∥BC交CD于N．则四边形PMNQ是平行四边形，即PQ∥MN．

解答 证明：过P作PM∥AD交D1D于M，过Q作QN∥BC交CD于N，连接MN．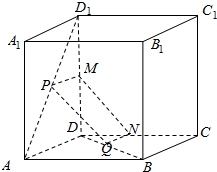

∵AD∥BC，
∴PM∥QN，
∵AD1=BD，AP=BQ
∴D1P=DQ，
∴$\frac{PM}{AD}$=$\frac{{D}_{1}P}{A{D}_{1}}$=$\frac{DQ}{BD}$=$\frac{QN}{BC}$，
∵AD=BC，
∴PM=QN．
∴四边形PMNQ是平行四边形，
∴PQ∥MN，?平面DCC1D1，
∵PQ?平面DCC1D1，
MN?平面DCC1D1，
∴PQ∥平面DCC1D1．

点评 本题考查了空间线面平行的判定，构造平行线是解题的关键．

练习册系列答案
相关题目
9．已知四边形ABCD是椭圆$\frac{{x}^{2}}{4}$+y2=1的内接菱形，则四边形ABCD的内切圆方程是（　　）
A．x2+y2=$\frac{1}{5}$B．（x-1）2+y2=$\frac{2}{5}$C．x2+y2=$\frac{4}{5}$D．x2+y2=$\frac{3}{5}$
10．函数y=$\frac{2}{1-\sqrt{1-x}}$的定义域为（　　）
A．（-∞，1）B．（-∞，0）∪（0，1]C．（-∞，0）∪（0，1）D．[1，+∞）
7．已知向量$\overrightarrow{m}$=（cosα，1-sinα），$\overrightarrow{n}$=（-cosα，sinα）（α∈R）．
（1）若$\overrightarrow{m}$⊥$\overrightarrow{n}$，求角α的值；
（2）若|$\overrightarrow{m}$-$\overrightarrow{n}$|=$\sqrt{3}$，求cos2α的值．
14．若g（x）=1-2x，f（g（x））=$\frac{1-x^2}{x^2}$，则f（$\frac{1}{2}$）的值为（　　）
A．1B．15C．4D．30
4．已知△ABC的外接圆半径为1，圆心为O，且3$\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=\overrightarrow{0}$，则△ABC的面积为（　　）
A．$\frac{8}{5}$B．$\frac{7}{5}$C．$\frac{6}{5}$D．$\frac{4}{5}$
11．已知函数f（x）=x2-2x（-1≤x≤2，x∈Z），则函数f（x）的值域是（　　）
A．[0，3]B．[-1，3]C．{-1，0，3}D．{0，1，3}
8．在（1+x+x2）n=D${\;}_{n}^{0}$+D${\;}_{n}^{1}$x+D${\;}_{n}^{2}$x2+…+D${\;}_{n}^{r}$xr+…+D${\;}_{n}^{2n-1}$x2n-1+D${\;}_{n}^{2n}$x2n的展开式中，把D${\;}_{n}^{0}$，D${\;}_{n}^{1}$，D${\;}_{n}^{2}$，…，D${\;}_{n}^{2n}$叫做三项式系数．
（1）当n=2时，写出三项式系数D${\;}_{2}^{0}$，D${\;}_{2}^{1}$，D${\;}_{2}^{2}$，D${\;}_{2}^{3}$，D${\;}_{2}^{4}$的值；
（2）类比二项式系数性质C${\;}_{n+1}^{m}$=C${\;}_{n}^{m-1}$+C${\;}_{n}^{m}$（1≤m≤n，m∈N，n∈N），给出一个关于三项式系数D${\;}_{n+1}^{m+1}$（1≤m≤2n-1，m∈N，n∈N）的相似性质，并予以证明；
（3）求D${\;}_{2015}^{0}$C${\;}_{2015}^{0}$-D${\;}_{2015}^{1}$C${\;}_{2015}^{1}$+D${\;}_{2015}^{2}$C${\;}_{2015}^{2}$-…+（-1）kD${\;}_{2015}^{k}$C${\;}_{2015}^{k}$+…+D${\;}_{2015}^{2014}$C${\;}_{2015}^{2014}$-D${\;}_{2015}^{2015}$C${\;}_{2015}^{2015}$的值．
9．已知函数$f（x）=cosx•\sqrt{\frac{1+sinx}{1-sinx}}+sinx•\sqrt{\frac{1+cosx}{1-cosx}}$
（1）当$x∈（0，\frac{π}{2}）$时，化简f（x）的解析式并求f（x）的对称轴和对称中心；
（2）当$x∈（π，\frac{3π}{2}）$时，求函数f（x）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网