Question

9．已知四边形ABCD是椭圆$\frac{{x}^{2}}{4}$+y²=1的内接菱形，则四边形ABCD的内切圆方程是（　　）

• A． x²+y²=$\frac{1}{5}$
• B． （x-1）²+y²=$\frac{2}{5}$
• C． x²+y²=$\frac{4}{5}$
• D． x²+y²=$\frac{3}{5}$

Answer 1

分析 由题意画出图形，求出原点到菱形边的距离得答案．

解答 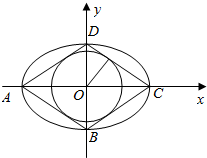解：如图，
由$\frac{{x}^{2}}{4}$+y²=1，得C（2，0），D（0，1），
∴CD所在直线方程为$\frac{x}{2}+y=1$，即x+2y-2=0，
原点O到直线x+2y-2=0的距离为d=$\frac{|-2|}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$，
即四边形ABCD的内切圆的半径为$\frac{2\sqrt{5}}{5}$．
∴四边形ABCD的内切圆方程是${x}^{2}+{y}^{2}=\frac{4}{5}$．
故选：C．

点评 本题考查椭圆的简单性质，考查数形结合的解题思想方法，是基础题．