题目内容
8.在△ABC中,内角A,B,C所对的边分别是a,b,c,若$tanA=\frac{1}{2}$,$tanB=\frac{1}{3}$,b=2,则tanC=-1,c=$2\sqrt{5}$.分析 由已知及两角和的正切函数公式,三角形内角和定理,诱导公式可求tanC的值,根据同角三角函数基本关系式可求sinB,sinC的值,利用正弦定理即可得解c的值.
解答 解:∵$tanA=\frac{1}{2}$,$tanB=\frac{1}{3}$,b=2,
∴tanC=tan(π-A-B)=-tan(A+B)=-$\frac{tanA+tanB}{1-tanAtanB}$=-$\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}×\frac{1}{3}}$=-1.
∵由$\frac{sinB}{\sqrt{1-si{n}^{2}B}}$=$\frac{1}{3}$,可得sinB=$\frac{\sqrt{10}}{10}$,由$\frac{sinC}{\sqrt{1-si{n}^{2}C}}$=-1,可得:sinC=$\frac{\sqrt{2}}{2}$,
∴由正弦定理可得:c=$\frac{b•sinC}{sinB}$=$\frac{2×\frac{\sqrt{2}}{2}}{\frac{\sqrt{10}}{10}}$=2$\sqrt{5}$.
故答案为:-1,2$\sqrt{5}$.
点评 本题主要考查了两角和的正切函数公式,三角形内角和定理,诱导公式,同角三角函数基本关系式,正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
18.椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1上点到直线x+2y-10=0的距离最小值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{6\sqrt{5}}{5}$ | D. | 0 |
19.圆C1:x2+y2-4x-2y+1=0与圆C2:x2+y2+4x-8y+11=0的位置关系为( )
| A. | 相交 | B. | 相离 | C. | 外切 | D. | 内切 |
16.设函数f(x)=2kx3+4(k-1)x2-3k2-2在区间(0,2)上是减函数,则k的取值范围是( )
| A. | $k<\frac{2}{5}$ | B. | $k≤\frac{2}{5}$ | C. | $0<k≤\frac{2}{5}$ | D. | $0≤k≤\frac{2}{5}$ |
3.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,且$\overrightarrow a$在$\overrightarrow b$方向上的投影与$\overrightarrow b$在$\overrightarrow a$方向上的投影相等,则$|{\overrightarrow a-\overrightarrow b}|$等于( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
13.正弦函数是奇函数,因为f(x)=sin(x+1)是正弦函数,所以f(x)=sin(x+1)是奇函数.以上推理( )
| A. | 结论正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 以上都不对 |
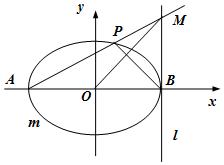 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.