题目内容
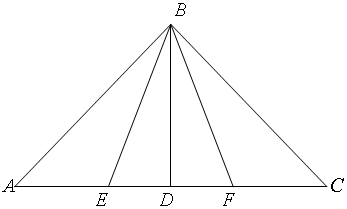
4.已知△ABC是等腰直角三角形,点E,F是斜边AC的三等分点,则tan∠EBF=( )| A. | $\frac{16}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{3}{4}$ |
分析 由题意,设AC=6,点E,F是斜边AC的三等分点,可得EF=2.过B点作AC的垂下交于D,利用三角函数的定义可得tan∠DBF的值,利用二倍角可得答案.
解答 解:由题意,设AC=6,点E,F是斜边AC的三等分点,可得EF=2.过B点作AC的垂下交于D,∠DBF=∠DBE.
∵△ABC是等腰直角三角形,
∴ AB=BC=$2\sqrt{3}$.DC=3
AB=BC=$2\sqrt{3}$.DC=3
由勾股定理,可得:DB=3.
那么:tan∠DBF=$\frac{1}{3}$.
∴tan∠EBF=tan2∠DBF=$\frac{2tan∠DBF}{1-ta{n}^{2}∠DBF}$=$\frac{3}{4}$.
故选:D.
点评 本题考查了三角函数的定义的运用和等腰直角三角形的性质.属于基础题.

练习册系列答案
相关题目
15.正方形ABCD,沿对角线BD折成直二面角A-BD-C,则折后的异面直线AB与CD所成的角的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.边长为2的正三角形ABC内(包括三边)有点P,$\overrightarrow{PB}$$•\overrightarrow{PC}$=1,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的范围是( )
| A. | [2,4] | B. | [$\frac{3-\sqrt{5}}{2}$,4] | C. | [3-$\sqrt{5}$,2] | D. | [$\frac{3-\sqrt{5}}{2}$,3-$\sqrt{5}$] |
19.圆C1:x2+y2-4x-2y+1=0与圆C2:x2+y2+4x-8y+11=0的位置关系为( )
| A. | 相交 | B. | 相离 | C. | 外切 | D. | 内切 |
9.已知曲线y=axcosx在$({\frac{π}{2},0})$处的切线的斜率为$\frac{1}{2}$,则实数a的值为( )
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{1}{π}$ | D. | $-\frac{1}{π}$ |
16.设函数f(x)=2kx3+4(k-1)x2-3k2-2在区间(0,2)上是减函数,则k的取值范围是( )
| A. | $k<\frac{2}{5}$ | B. | $k≤\frac{2}{5}$ | C. | $0<k≤\frac{2}{5}$ | D. | $0≤k≤\frac{2}{5}$ |
13.正弦函数是奇函数,因为f(x)=sin(x+1)是正弦函数,所以f(x)=sin(x+1)是奇函数.以上推理( )
| A. | 结论正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 以上都不对 |