题目内容
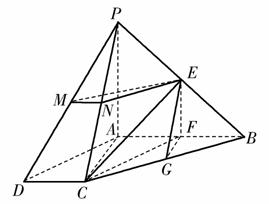
如图，四棱锥P－ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．
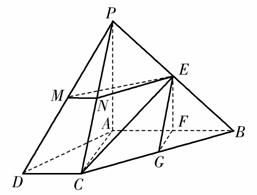
(1)求证：CE∥平面PAD；
(2)求证：平面EFG⊥平面EMN.
[解析] (1)解法一：取PA的中点H，连接EH，DH.
因为E为PB的中点，
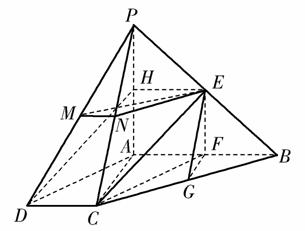
所以EH∥AB，EH＝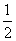
AB.
又AB∥CD，CD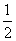＝AB，所以EH∥CD，EH＝CD.
因此四边形DCEH是平行四边形．所以CE∥DH.
又DH⊂平面PAD，CE⊄平面PAD，
因此CE∥平面PAD.
解法二：连接CF.
因为F为AB的中点，所以AF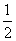＝AB.
又CD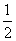＝AB，所以AF＝CD.
又AF∥CD，所以四边形AFCD为平行四边形．
因此CF∥AD.
又CF⊄平面PAD，所以CF∥平面PAD.
因为E、F分别为PB、AB的中点，所以EF∥PA.
又EF⊄平面PAD，所以EF∥平面PAD.
因为CF∩EF＝F，故平面CEF∥平面PAD.
又CE⊂平面CEF，所以CE∥平面PAD.
(2)证明：因为E、F分别为PB、AB的中点，
所以EF∥PA.
又AB⊥PA，所以AB⊥EF.
同理可证AB⊥FG.
又EF∩FG＝F，EF⊂平面EFG，FG⊂平面EFG，
因此AB⊥平面EFG.
又M、N分别为PD、PC的中点，
所以MN∥CD.
又AB∥CD，所以MN∥AB.
因此MN⊥平面EFG.
又MN⊂平面EMN，
所以平面EFG⊥平面EMN.
练习册系列答案
相关题目
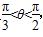，则其侧面展开图中心角α满足( )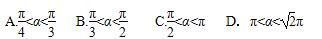
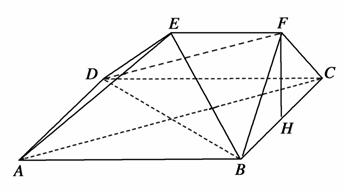
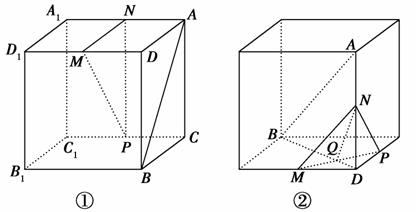
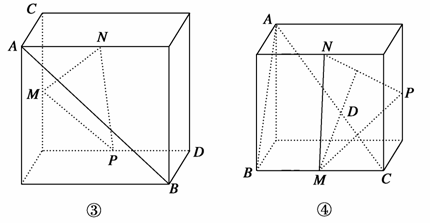
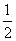(AC＋BD)(填“>”，“<”或“＝”)．