题目内容
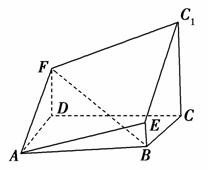
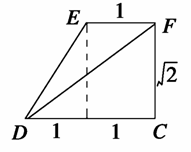
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点.
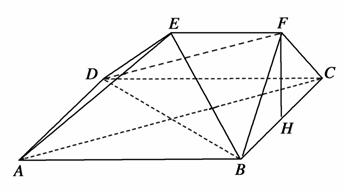
(1)求证:FH∥平面EDB;
(2)求证:AC⊥平面EDB;
(3)求四面体B-DEF的体积.
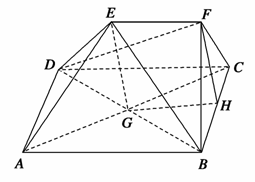
[解析] (1)证明:设AC与BD交于点G,联结EG、GH.
则G为AC中点,∵H是BC中点,
∴GH綊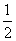 AB,又∵EF綊
AB,又∵EF綊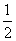 AB,
AB,
∴四边形EFHG为平行四边形.∴FH∥EG.
又EG⊂平面EDB,而FH⊄平面EDB,
∴FH∥平面EDB.
(2)证明:∵EF∥AB,EF⊥FB.∴AB⊥FB.
又四边形ABCD为正方形,
∴AB⊥BC,又FB∩BC=B,∴AB⊥平面BFC.
∵FH⊂平面BFC,∴AB⊥FH.
又∵FB=FC,H是BC中点,∴FH⊥BC.
又AB∩BC=B,∴FH⊥平面ABCD,∴FH⊥AC.
又EG∥FH,∴EG⊥AC,
又AC⊥BD,BD∩EG=G,∴AC⊥平面EDB.
(3)∵EF⊥BF,BF⊥FC且EF∩FC=F,
∴BF⊥平面CDEF,
即BF⊥平面DEF.
∴BF为四面体B—DEF的高.
又∵BC=AB=2,∴BF=FC=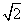 .
.
四边形CDEF为直角梯形,且EF=1,CD=2.
∴S△DEF=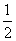 (1+2)×
(1+2)×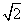 -
-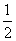 ×2×
×2×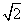 =
=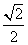

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目