题目内容
由下列不等式:1>
,1+
+
>1,1+
+
+…+
>
,1+
+
+…+
>2,…,你能猜想得到一个怎样的一般不等式?用数学归纳法证明你的结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 7 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
考点:数学归纳法,归纳推理
专题:点列、递归数列与数学归纳法
分析:根据已知不等式猜想第n个不等式,然后利用数学归纳法证明即可.
解答:
解:根据给出的几个不等式不等式:1>
,1+
+
>1,1+
+
+…+
>
,1+
+
+…+
>2,…,
即一般不等式为:1+
+
+…+
>
.
用数学归纳法证明如下:
①当n=1时,1>
,猜想正确.
②假设n=k时猜想成立,即不等式:1+
+
+…+
>
,
则n=k+1时,1+
+
+…+
+
+
+
+…+
>
+
+
+…+
>
+
+
+…+
=
+
=
+
=
,
即当n=k+1时,猜想也成立,
所以对任意的n∈N+,不等式成立.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 7 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
即一般不等式为:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| n |
| 2 |
用数学归纳法证明如下:
①当n=1时,1>
| 1 |
| 2 |
②假设n=k时猜想成立,即不等式:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2k-1 |
| k |
| 2 |
则n=k+1时,1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2k-1 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| 2k+1-1 |
| k |
| 2 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+1-1 |
>
| k |
| 2 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| k |
| 2 |
| 2k |
| 2k+1 |
| k |
| 2 |
| 1 |
| 2 |
| k+1 |
| 2 |
即当n=k+1时,猜想也成立,
所以对任意的n∈N+,不等式成立.
点评:本题考查数学猜想,以及数学归纳法的证明,特别注意n=k+1时不等式两边项数的变化,并且必须用上假设,考查逻辑思维能力,计算能力.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
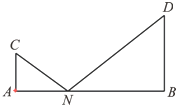 如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.
如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.