题目内容
设g(x)=|f(x+2m)-x|,f(t)为不超过实数t的最大整数,若函数g(x)存在最大值,则正实数m的最小值为 ( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:由题意知,当n-1≤x+2m<n,(n∈Z)时,f(x+2m)=n-1;从而可化简得2m-1<f(x+2m)-x≤2m,再由最值可得2m≥|2m-1|;从而求得.
解答:
解:∵f(t)为不超过实数t的最大整数,
∴当n-1≤x+2m<n,(n∈Z)时,f(x+2m)=n-1;
故n-1-2m≤x<n-2m;
故2m-1<f(x+2m)-x≤2m;
又∵m>0;
故若函数g(x)存在最大值,
则2m≥|2m-1|;
故m≥
;
故选D.
∴当n-1≤x+2m<n,(n∈Z)时,f(x+2m)=n-1;
故n-1-2m≤x<n-2m;
故2m-1<f(x+2m)-x≤2m;
又∵m>0;
故若函数g(x)存在最大值,
则2m≥|2m-1|;
故m≥
| 1 |
| 4 |
故选D.
点评:本题考查了绝对值函数与分段函数的应用,属于中档题.

练习册系列答案
相关题目
某程序框图如图所示,则输出的结果S=( )
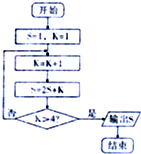

| A、11 | B、26 | C、57 | D、120 |
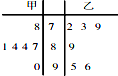 甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )
甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )| A、甲乙同学的平均成绩相同,但是甲同学的成绩比乙稳定 |
| B、甲乙同学的平均成绩相同,但是乙同学的成绩比甲稳定 |
| C、甲同学的平均成绩比乙同学好,但是乙同学的成绩比甲稳定 |
| D、乙同学的平均成绩比甲同学好,但是甲同学的成绩比乙稳定 |
设i为虚数单位,则复数
=( )
| 3-4i |
| i |
| A、-4-3i | B、-4+3i |
| C、4+3i | D、4-3i |