题目内容
2. 如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为
如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为等边三角形,M为△ABC内部一点,点P在OM的延长线上,且OM=$\frac{1}{3}$MP,PA=PB.
(1)证明:AB⊥平面POC;
(2)求三棱锥A-PBC的体积.
分析 (1)证明AB⊥OC,AB⊥PO,即可证明AB⊥平面POC;
(2)利用等体积转换,即可求三棱锥A-PBC的体积.
解答 (1) 证明:因为三棱锥O-ABC的三条棱OA,OB,OC,
证明:因为三棱锥O-ABC的三条棱OA,OB,OC,
所以OC⊥OA,OC⊥OB,
因为OA∩OB=O,所以OC⊥平面OAB,
而AB?平面OAB,所以AB⊥OC. …(2分)
取AB中点D,连结OD,PD.由OA=OB有AB⊥OD.
由PA=PB有AB⊥PD. …(3分)
因为OD∩PD=D,所以AB⊥平面POD,
而PO?平面POD,所以AB⊥PO. …(5分)
因为OC∩OP=O,所以AB⊥平面POC,…(6分)
(2)解:由已知可得VC-OAB=$\frac{1}{3}{S}_{△OAB}•OC$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\sqrt{2}$=$\frac{\sqrt{2}}{3}$,…(8分)
且AB=AC=BC=2
∴S△ABC=$\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$ …(9分)
设点O、P到平面ABC的距离分别为h1,h2,
由VO-ABC=VC-OAB得,$\frac{1}{3}$S△ABCh1=$\frac{\sqrt{2}}{3}$,则h1=$\frac{\sqrt{6}}{3}$ …(10分)
∵$\frac{{h}_{1}}{{h}_{2}}$=$\frac{OM}{MP}$=$\frac{1}{3}$,∴h2=$\sqrt{6}$ …(11分)
∴VA-PBC=VP-ABC=$\frac{1}{3}$S△ABCh2=$\frac{1}{3}×\sqrt{3}×\sqrt{6}$=$\sqrt{2}$ …(12分)
点评 本题考查线面垂直的判定与性质,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

| A. | {x|x≤0} | B. | {x|1≤x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x<或x≥2} |
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
| A. | 2n-1 | B. | 3n-1 | C. | 2n | D. | 3n |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 ,点
,点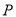 是
是 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点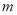 .
.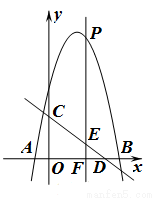
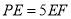 ,求
,求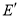 是点
是点 关于直线
关于直线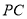 的对称点、是否存在点
的对称点、是否存在点 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点