题目内容
已知直线(1-λ)x+(3λ+1)y-4=0(λ∈R)所过定点恰好落在曲线f(x)=
上,若函数h(x)=f(x)-mx+2有三个不同的零点,则实数m的范围是( )
|
A、(
| ||
B、(-∞,
| ||
C、(-∞,
| ||
D、(
|
考点:分段函数的应用
专题:函数的性质及应用
分析:根据直线过定点,求出定点坐标,从而求出a,作出函数f(x)的图象,利用数形结合即可得到结论.
解答:
解:依题意,直线为(x+y-4)-λ(x-3y)=0,联立
,
解得
,故定点为(3,1),loga3=1,
∴a=3,f(x)=
.
令h(x)=f(x)-mx+2=0,
故f(x)=mx-2.则f(x)的图象与g(x)=mx-2的图象有三个不同的交点.
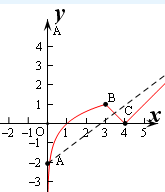
作图,得关键点A(0,-2),B(3,1),C(4,0),
可知g(x)=mx-2应介于直线AB与直线AC之间.
由kAB=1,kAC=
,故m∈(
,1).
故选:A
|
解得
|
∴a=3,f(x)=
|

令h(x)=f(x)-mx+2=0,
故f(x)=mx-2.则f(x)的图象与g(x)=mx-2的图象有三个不同的交点.
作图,得关键点A(0,-2),B(3,1),C(4,0),
可知g(x)=mx-2应介于直线AB与直线AC之间.
由kAB=1,kAC=
| 1 |
| 2 |
| 1 |
| 2 |
故选:A
点评:本题主要考查函数零点个数的应用,利用分段函数的表达式,结合数形结合是解决本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
设x>0,P=2x+2-x,Q=1+2x-x2,则( )
| A、P≥Q | B、P≤Q |
| C、P>Q | D、P<Q |
下列函数中,既是偶函数又在区间(0,+∞)上单调递增的函数是( )
| A、y=log2(x+1) |
| B、y=|x|+1 |
| C、y=-x2+1 |
| D、y=2-|x| |
命题p:直线ax+by+c=0与圆x2+y2=1恰有一个公共点,命题q:a,b,c为直角三角形的三条边,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设l,m是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )
| A、若l∥m,m?β,则l∥β |
| B、若l∥α,m∥α,则l∥m |
| C、若α⊥γ,β⊥γ,α∩β=l,则l⊥γ |
| D、若l∥α,l∥β,则α∥β |
下列命题中逆命题为真命题的是( )
(1)若x2-3x+2=0,则x=1或x=2;
(2)若-2≤x<3,则(x+2)(x-3)≤0;
(3)若x=y=0,则x2+y2=0
(4)已知x,y∈N*,若x,y是偶数,则x+y是偶数.
(1)若x2-3x+2=0,则x=1或x=2;
(2)若-2≤x<3,则(x+2)(x-3)≤0;
(3)若x=y=0,则x2+y2=0
(4)已知x,y∈N*,若x,y是偶数,则x+y是偶数.
| A、(1)(3) | B、(2) |
| C、(3) | D、(4) |
三角形ABC中,若
•
=
•
=
•
,则三角形ABC的形状是( )
| BC |
| CA |
| CA |
| AB |
| AB |
| BC |
| A、等边三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |
圆锥曲线
+
=1的离心率e=
,则a的值为( )
| y2 |
| 9 |
| x2 |
| a+8 |
| 1 |
| 2 |
| A、4 | ||||
B、-
| ||||
C、4或-
| ||||
| D、以上均不正确 |