题目内容
已知圆C的圆心在直线2x-y-7=0上并与y轴交于两点A(0,-4),B(0,-2),求圆C的方程.
考点:圆的标准方程
专题:直线与圆
分析:设圆C的方程为(x-a)2+(y-b)2=r2,由此利用待定系数法能求出圆C的方程.
解答:
解:设圆C的方程为(x-a)2+(y-b)2=r2,
由已知得
,
解得a=2,b=-3,r2=5,
∴圆C的方程(x-2)2+(y+3)2=5.
由已知得
|
解得a=2,b=-3,r2=5,
∴圆C的方程(x-2)2+(y+3)2=5.
点评:本题考查圆的方程的求法,是基础题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}的通项式an=
,则数列{an}中的最大项是( )
| n |
| n2+90 |
| A、第9项 |
| B、第10项和第9项 |
| C、第10项 |
| D、第9项和第8项 |
方程2a•9sinx+4a•3sinx+a-8=0有解,则a的取值范围是( )
A、
| ||||
| B、a>0 | ||||
C、0<a≤
| ||||
| D、a>0或a≤-8 |
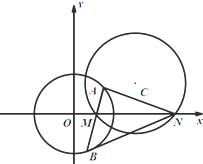 在△ABC中,a,b,c分别是角A,B,C的对边,C=2A,cosA=
在△ABC中,a,b,c分别是角A,B,C的对边,C=2A,cosA= 如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20m,求山高CD.
如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20m,求山高CD.