题目内容
复数z满足zi=1+3i，则z在复平面内所对应的点的坐标是（ ）
| A、（1，-3） |
| B、（-1，3） |
| C、（-3，1） |
| D、（3，-1） |
考点：复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：利用复数的运算法则即可得出．
解答：
解：∵复数z满足zi=1+3i，
∴-i•i•z=-i（1+3i），
化为z=3-i．
∴z在复平面内所对应的点的坐标是（3，-1）．
故选：D．
∴-i•i•z=-i（1+3i），
化为z=3-i．
∴z在复平面内所对应的点的坐标是（3，-1）．
故选：D．
点评：本题考查了复数的运算法则，属于基础题．
练习册系列答案
相关题目
一个均匀小正方体的六个面中，三个面上标以数0，两个面上标以数1，一个面上标以数3，将这个小正方体抛掷两次，则向上的数之积的数学期望是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数x、y满足不等式组
，且ax+by≤1，（a＞0，b＞0）恒成立，则a+b的取值范围是（ ）
|
| A、（0，4] | ||
B、（0，
| ||
| C、（0，2） | ||
D、[
|
对任意实数x，都有（x-1）11=a0+a1（x-3）+a2（x-3）2+a3（x-3）3+…+a11（x-3）11，则
=（ ）
| a1+a3+a5+a7+a11 |
| a9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知不等式组
，则其表示的平面区域的面积是（ ）
|
| A、1 | B、2 | C、3 | D、4 |
如图所给的程序运行结果为S=35，那么判断框中应填入的关于k的条件是（ ）
| A、k=7 | B、k≤6 |
| C、k＜6 | D、k＞6 |
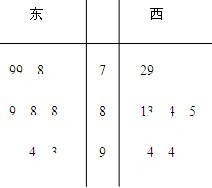某城市要建成宜商、宜居的国际化新城，该城市的东城区、西城区分别引进8个厂家，现对两个区域的16个厂家进行评估，综合得分情况如茎叶图所示．