题目内容
20.在区间[0,2π]上随机地取一个数x,则事件“2sinx<1”发生的概率为$\frac{2}{3}$.分析 利用几何概型的概率公式、对立事件的概率公式进行求解即可.
解答 解:当0≤x≤2π时,由2sinx≥1得$\frac{π}{6}$≤x≤$\frac{5π}{6}$,
则事件“2sinx≥1”发生的概率为$\frac{\frac{5π}{6}-\frac{π}{6}}{2π}$=$\frac{1}{3}$
∴事件“2sinx<1”发生的概率为P=1-$\frac{1}{3}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题主要考查几何概型的概率的计算,根据三角函数的性质求出2sinx≥1的解是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知角θ满足sinθ-2cosθ=0,则$\frac{{cos(\frac{3π}{2}+θ)+4cos(π-θ)}}{{sin(\frac{π}{2}-θ)-sin(π-θ)}}$=( )
| A. | -2 | B. | 0 | C. | $\frac{2}{3}$ | D. | 2 |
11.执行如图所示的程序框图,则输出的i值为( )
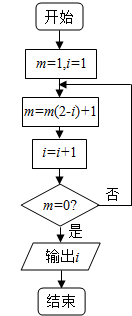

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.已知集合A={x|x>1},B={x|(x+1)(x-2)<0},则A∪B=( )
| A. | {x|x>-1} | B. | {x|-1<x≤1} | C. | {x|-1<x<2} | D. | {x|1<x<2} |
12.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,m),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则m的值为( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
 执行如图所示的程序框图,设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出的S的值为n,则m+n=14.
执行如图所示的程序框图,设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出的S的值为n,则m+n=14.