题目内容
10.已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN切于点B,过M,N与圆C相切的 两直线相交于P点,则点P的轨迹方程为${x}^{2}-\frac{{y}^{2}}{8}=1$(x>1).分析 PM,PN分别与圆C相切于R、Q,根据圆的切线长定理,能够推导出PM-PN=QM-RN=MB-NB=2<MN,因此点P的轨迹是以M、N为焦点的双曲线.再根据题条件能够求出P点的轨迹方程.
解答 解:由已知,设PM,PN分别与圆C相切于R、Q,
根据圆的切线长定理,有PQ=PR,MQ=MB,NR=NB;
∴PM-PN=QM-RN=MB-NB=2<MN
∴点P的轨迹是以M、N为焦点的双曲线的右支,c=3,a=1,所以b2=8
∴点P的轨迹方程为:${x}^{2}-\frac{{y}^{2}}{8}=1$(x>1).
故答案为:${x}^{2}-\frac{{y}^{2}}{8}=1$(x>1).
点评 本题考查双曲线的基本性质和圆的切线长定理,正确运用双曲线的定义是关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
1.已知四面体ABCD的顶点A,B,C,D在空间直角坐标系中的坐标分别为$(1,0,0),(0,1,0),(0,0,1),(-\frac{1}{3},-\frac{1}{3},-\frac{1}{3})$,O为坐标原点,则在下列命题中,正确的为( )
| A. | OD⊥平面ABC | B. | 直线OB∥平面ACD | ||
| C. | 直线AD与OB所成的角是45° | D. | 二面角D-OB-A为45° |
18.已知函数f(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+4b的取值范围是( )
| A. | (4,+∞) | B. | [4,+∞) | C. | (5,+∞) | D. | [5,+∞) |
15.已知点A是抛物线y=$\frac{1}{4}{x^2}$的对称轴与准线的交点,点B为该抛物线的焦点,点P在该抛物线上且满足|PB|=m|PA|,当m取最小值时,点P恰好在以A,B为焦点的双曲线上,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{2}+1}}{2}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{5}-1$ |
2.“女大学生就业难”究竟有多难?其难在何处?女生在求职中是否收到了不公平对待?通过对某大学应届毕业生的调查与实证分析试对下列问题提出解答.为调查某地区大学应届毕业生的调查,用简单随机抽样方法从该地区抽取了500为大学生做问卷调查,结果如下:
(1)估计该地区大学生中,求职中收到了公平对待的学生的概率;
(2)能否有99%的把握认为该地区的大学生求职中受到了不公平对待与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的大学生中,求职中是否受到了不公平对待学生的比例?说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 性别 是否公平 | 男 | 女 |
| 公平 | 40 | 30 |
| 不公平 | 160 | 270 |
(2)能否有99%的把握认为该地区的大学生求职中受到了不公平对待与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的大学生中,求职中是否受到了不公平对待学生的比例?说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.000 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
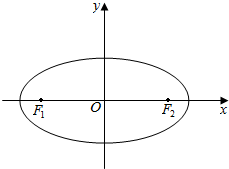 平面直角坐标系x0y中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,左、右焦点分别是F1,F2,以F1为圆心以3为半径的圆与以F2为圆心以1为半径的圆相交,且交点在椭圆C上.
平面直角坐标系x0y中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,左、右焦点分别是F1,F2,以F1为圆心以3为半径的圆与以F2为圆心以1为半径的圆相交,且交点在椭圆C上.