题目内容
已知函数f(x)=elnx,g(x)=
f(x)-(x+1)(e为自然对数).
(1)求函数g(x)的最大值;
(2)求证:e 1+
+
+…
>n+1(n∈N*)
| 1 |
| e |
(1)求函数g(x)的最大值;
(2)求证:e 1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
考点:导数在最大值、最小值问题中的应用,不等式的证明
专题:函数的性质及应用,导数的综合应用
分析:(1)求g′(x)=
,容易求出g(x)在(0,+∞)上的极大值,也是最大值为g(1)=-2;
(2)要证明原不等式成立,只需先证明1+
+
+…+
>ln(n+1).而由(1)知lnx-(x+1)≤-2,所以x-1≥lnx,当且仅当x=1时取“=”,令x-1=t,x=t+1,所以t≥ln(t+1),取t=
,便得到
>ln(
+1)=ln(
),这样让n从1取到n,把得到的不等式的左右两边同时相加便可得:1+
+
+…+
>ln(n+1),对不等式两边同时取以e为底的指数便得到原不等式.
| 1-x |
| x |
(2)要证明原不等式成立,只需先证明1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| n+1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
解答:
解:(1)g(x)=lnx-(x+1),g′(x)=
-1=
;
∴x∈(0,1)时,g′(x)>0;x∈(1,+∞)时,g′(x)<0;
∴x=1时,g(x)取得极大值,也是最大值-2;
(2)由(1)知,对任意的x∈(0,+∞),lnx-(x+1)≤-2,即:
lnx≤x-1,当且仅当x=1时取“=”,令x-1=t,x=t+1,则:
ln(t+1)≤t,即t≥ln(t+1),取t=
,n∈N*,则:
>ln(
+1)=ln(
);
∴1>ln2;
>ln
;
>ln
;
…
>ln(
)
∴1+
+
+…+
>ln(2•
•
…
)=ln(n+1);
∴e1+
+
+…+
>n+1.
| 1 |
| x |
| 1-x |
| x |
∴x∈(0,1)时,g′(x)>0;x∈(1,+∞)时,g′(x)<0;
∴x=1时,g(x)取得极大值,也是最大值-2;
(2)由(1)知,对任意的x∈(0,+∞),lnx-(x+1)≤-2,即:
lnx≤x-1,当且仅当x=1时取“=”,令x-1=t,x=t+1,则:
ln(t+1)≤t,即t≥ln(t+1),取t=
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| n+1 |
| n |
∴1>ln2;
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
…
| 1 |
| n |
| n+1 |
| n |
∴1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 4 |
| 3 |
| n+1 |
| n |
∴e1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
点评:考查极值的概念,根据极值求函数的最值,对数的运算,以及指数函数、对数函数的单调性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等比数列{an}中,a2=10,a3=20,则a4等于( )
| A、70 | B、40 | C、30 | D、90 |
函数f(x)=
(x∈[1,2])的最大值是( )
| 1 |
| 1-x+x2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如下:
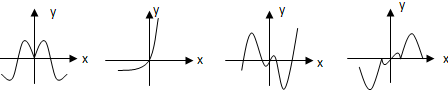
则按照从左到右图象对应的函数序号安排正确的一组是( )

则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |

 在抛物线y2=16x内有一点G(4,4)抛物线的焦点为F,若以F,G为焦点作一个与抛物线相交且长轴最短的椭圆,则此椭圆的离心率为
在抛物线y2=16x内有一点G(4,4)抛物线的焦点为F,若以F,G为焦点作一个与抛物线相交且长轴最短的椭圆,则此椭圆的离心率为