题目内容
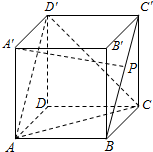 如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题:
如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题:①A′P与CD一定是异面直线;
②A′P⊥B′D;
③三棱锥A-D′PC的体积不变;
其中正确的是
考点:空间中直线与直线之间的位置关系,棱柱的结构特征,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:当点P是CC′中点时,A′D∥PC,故①不正确;以D为原点,建立空间直角坐标系,用向量法能证明DB′⊥A′BC′,从而得到A′P⊥B′D,故②正确;由已知条件推导出BC′∥平面AD′C,又P∈BC′,所以三棱锥A-D′PC的体积不变,故③正确.
解答:
解:当点P是CC′中点时,
A′D∥PC,此时A′P与CD共面于平面A′DCP,
故①不正确;
以D为原点,建立空间直角坐标系,
设正方体的棱长为1,
则D(0,0,0),B′(1,1,1),A′(1,0,1),
B(1,1,0),C′(0,1,1),
∴
=(1,1,1),
=(0,1,-1),
=(-1,1,0),
∴
•
=0,
•
=0,
∴DB′⊥A′B,DB′⊥A′C′,
∵A′B∩A′C′=A′,∴DB′⊥A′BC′,
∵A′P?平面A′BC′,∴A′P⊥B′D,
故②正确;
∵AD′∥BC′,AD′?平面AD′C,BC′不包含于平面AD′C,
∴BC′∥平面AD′C,又P∈BC′,
∴三棱锥A-D′PC的体积不变,
故③正确.
故答案为:②③.

A′D∥PC,此时A′P与CD共面于平面A′DCP,
故①不正确;
以D为原点,建立空间直角坐标系,
设正方体的棱长为1,
则D(0,0,0),B′(1,1,1),A′(1,0,1),
B(1,1,0),C′(0,1,1),
∴
| DB′ |
| A′B |
| A′C′ |
∴
| DB′ |
| A′B |
| DB′ |
| A′C′ |
∴DB′⊥A′B,DB′⊥A′C′,
∵A′B∩A′C′=A′,∴DB′⊥A′BC′,
∵A′P?平面A′BC′,∴A′P⊥B′D,
故②正确;
∵AD′∥BC′,AD′?平面AD′C,BC′不包含于平面AD′C,
∴BC′∥平面AD′C,又P∈BC′,
∴三棱锥A-D′PC的体积不变,
故③正确.
故答案为:②③.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
若a>b>0,则下列不等式成立的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|