题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,若bcosA+acosB=
c•cosB,则角B的大小是 .
| 2 |
考点:正弦定理
专题:
分析:利用正弦定理把已知等式中的边化成角的正弦,利用两角和公式进行化简求得cosB的值.则B可求得.
解答:
解:∵bcosA+acosB=
c•cosB,
∴sinBcosA+sinAcosB=sin(A+B)=sinC=
sinCcosB,
∵sinC≠0,
∴cosB=
,
∴B=
.
故答案为:
| 2 |
∴sinBcosA+sinAcosB=sin(A+B)=sinC=
| 2 |
∵sinC≠0,
∴cosB=
| ||
| 2 |
∴B=
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题主要考查了正弦定理的应用.解题的关键时利用正弦定理完成边角问题的转化.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
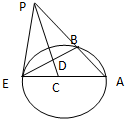 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=40°,则∠PCE等于
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=40°,则∠PCE等于
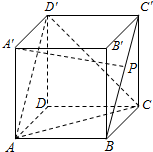 如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题:
如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题: 如图,M是抛物线y2=4x上一点,F是抛物线的焦点,若∠MFO=120°,则MF=
如图,M是抛物线y2=4x上一点,F是抛物线的焦点,若∠MFO=120°,则MF=