题目内容
若(x2+1)(2x-3)9=a0+a1x+a2x2+…+a11x11,则a0+a1+a2+…+a11的值为 .
考点:二项式系数的性质
专题:二项式定理
分析:在所给的等式中,令x=1可得a0+a1+a2+…+a11的值.
解答:
解:在(x2+1)(2x-3)9=a0+a1x+a2x2+…+a11x11中,
令x=1可得a0+a1+a2+…+a11=-2,
故答案为:-2.
令x=1可得a0+a1+a2+…+a11=-2,
故答案为:-2.
点评:本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于基题.

练习册系列答案
相关题目
在△ABC中,已知A=60°,B=45°,a=8,则b=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、8
|
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.则f(20)等于( )


| A、761 | B、762 |
| C、841 | D、842 |
若5名学生排成一列,则其中学生甲站在最左边的排法种数为( )
| A、10 | B、48 | C、120 | D、24 |
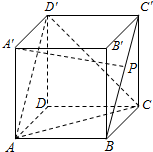 如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题:
如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题: 如图,M是抛物线y2=4x上一点,F是抛物线的焦点,若∠MFO=120°,则MF=
如图,M是抛物线y2=4x上一点,F是抛物线的焦点,若∠MFO=120°,则MF=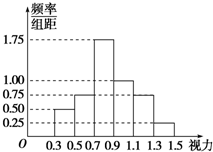 从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,按视力分六组(0.3,0.5],(0.5,0.7],(0.7,0.9],(0.9,1.1](1.1,1.3],(1.3,1.5].其结果的频率分布直方图如图所示:若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为
从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,按视力分六组(0.3,0.5],(0.5,0.7],(0.7,0.9],(0.9,1.1](1.1,1.3],(1.3,1.5].其结果的频率分布直方图如图所示:若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为