Question

已知函数f（x）=（x²-

3

2

x）e^mx
（Ⅰ）若函数f（x）在区间（1，+∞）上只有一个极值点，求实数m的取值范围．
（Ⅱ）若函数f（x）中m=1时，函数g（x）=kx+1（k≠0），且?x₁∈[-

3

2

，2]，?x₂∈[2，3]使得f（x）≥g（x）成立．求实数k的取值范围．

Answer 1

考点：利用导数研究函数的极值,利用导数研究函数的单调性

专题：导数的综合应用

分析：（Ⅰ）由已知推得f′（x）=0⇒mx²+

4-3m

2

x-

3

2

=0，由m的值分情况讨论可得实数m的取值范围；
（Ⅱ）当m=1则f′（x）=

1

2

e^x•（2x²+x-3），?x₁∈[-

3

2

，2]，?x₂∈[2，3]，k＜0时，有-

e

2

≥2k+1，从而求得实数k的取值范围．

解答： 解：（Ⅰ）∵f′（x）=e^mx•[mx²+

4-3m

2

x-

3

2

]
∴f′（x）=0⇒mx²+

4-3m

2

x-

3

2

=0
①当m=0则x=

3

4

∉（1，+∞），故不合题意；
②当m＞0，若f（x）在（1，+∞）只有一个极值点，则只需满足f′（x）＜0即可，⇒m+

4-3m

2

-

3

2

＜0，故m＞1；
③当m＜0则需满足f′（1）＞0即可，⇒m＜1，故m＜0．
综上可得：m取值范围为：m＞1或m＜0．
（Ⅱ）当m=1则f（x）=（x²-

3

2

x）e^x
则有f′（x）=

1

2

e^x•（2x²+x-3）
若?x₁∈[-

3

2

，2]，?x₂∈[2，3]有f（x₁）≥g（x₂）成立，则只需f（x）_min≥g（x）_max即可．
令f′（x）=0，故x=-

3

2

或x=1
故

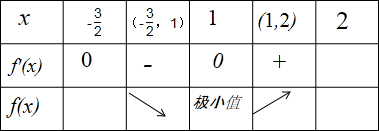
∴f（x）_极小值=f（1）=-

e

2

故有：当k＞0时，g（x）_max=g（3）=3k+1，此时-

e

2

≥3k+1不可能成立；
当k＜0时，g（x）_max=g（2）=2k+1，此时有-

e

2

≥2k+1，
从而解得k≤-

1

2

-

e

4

．

点评：本题主要考察了利用导数研究函数的极值和单调性，考察了导数的综合应用，属于难题．