题目内容
设p:2x2-3x+1≤0,q:x2-(2a+1)x+a2+a≤0,若?p是?q的必要而不充分条件,则实数a的取值范围是 ( )
A、[0,
| ||
B、(0,
| ||
C、(-∞,0]∪[
| ||
D、(-∞,0)∪(
|
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先写出¬p,¬q,并解出¬p,¬q下的不等式,从而得到¬p:x<
,或x>1,¬q:x<a,或x>a+1,根据¬p是¬q的必要不充分条件得出限制a的不等式,解不等式即得a的取值范围.
| 1 |
| 2 |
解答:
解:¬p:2x2-3x+1>0,¬q:x2-(2a+1)x+a2+a>0;
解2x2-3x+1>0得x<
,或x>1,解x2-(2a+1)x+a2+a>0得x<a,或x>a+1;
若?p是?q的必要而不充分条件;
∴
,解得0≤a≤
,即实数a的取值范围是[0,
].
故选A.
解2x2-3x+1>0得x<
| 1 |
| 2 |
若?p是?q的必要而不充分条件;
∴
|
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:考查由命题p,q求¬p,¬q,解一元二次不等式,必要条件,充分条件,必要不充分条件的概念.

练习册系列答案
相关题目
下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
A、f(x)=x
| ||
| B、f(x)=x3 | ||
C、f(x)=(
| ||
| D、f(x)=3x |
某几何体的三视图如图所示,则该几何体的体积为( )
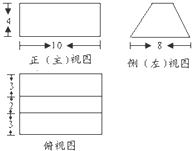

| A、240 | ||
| B、200 | ||
C、
| ||
D、
|