题目内容
12.一个袋中装有四个大小、形状完全相同的小球,小球的编号分别为1,2,3,4.(Ⅰ)从袋中随机取两个小球,求取出的两个小球的编号之和不小于5的概率;
(Ⅱ)先从袋中随机取一个小球,记此小球的编号为m,将此小球放回袋中,然后再从袋中随机取一个小球,记该小球的编号为n,求n=m+2的概率.
分析 (Ⅰ)从袋中随机取两个小球,利用列举法能求出取出的两个小球的编号之和不小于5的概率.
(Ⅱ)先从袋中随机选一个小球,记下编号为m,放回后,再从袋中随机取一个小球,记下编号为n,利用列举法能求出满足条件n=m+2的概率.
解答 解:(Ⅰ)从袋中随机取两个小球,所有可能结果的基本事件为:
{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,
设“取出的两个小球的编号之和不小于5”为事件A,事件A包含的基本事件为:
{1,4},{2,3},{2,4},{3,4},共4个,
∴所求事件的概率P(A)=$\frac{4}{6}=\frac{2}{3}$.
(Ⅱ)先从袋中随机选一个小球,记下编号为m,放回后,再从袋中随机取一个小球,记下编号为n,
其一切可能的结果记为(m,n),则有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个,
设“满足条件n=m+2”的事件的概率为P(B)=$\frac{2}{16}=\frac{1}{8}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
2.设P,Q分别为圆x2+(y-3)2=5和椭圆$\frac{x^2}{10}$+y2=1上的点,则P,Q两点间的最大距离是( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{19}$+$\sqrt{2}$ | C. | 4+$\sqrt{5}$ | D. | 3$\sqrt{5}$ |
3.定义域为[a,b]的函数y=f(x)图象的两个端点为A、B,M(x,y)是f(x)图象上任意一点,其中x=λa+(1-λ)b,λ∈[0,1].已知向量$\overrightarrow{ON}$=$λ\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$,若不等式|$\overrightarrow{MN}$|≤k恒成立,则称函数f(x)在[a,b]上“k阶线性近似”,若函数y=x-$\frac{2}{x}$在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
| A. | [$\sqrt{2}$-1,+∞) | B. | [$\sqrt{2}$+1,+∞) | C. | [3-2$\sqrt{2}$,+∞) | D. | [3+2$\sqrt{2}$,+∞) |
20.在平行六面体ABCD-A1B1C1D1中,化简$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{A{A}_{1}}$=( )
| A. | $\overrightarrow{A{C}_{1}}$ | B. | $\overrightarrow{C{A}_{1}}$ | C. | $\overrightarrow{B{C}_{1}}$ | D. | $\overrightarrow{C{B}_{1}}$ |
1.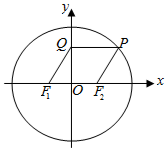 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )
 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |