题目内容
17．已知a，b，c为直角三角形中的三边长，c为斜边长，若点M（m，n）在直线l：ax+by+2c=0上，则m2+n2的最小值为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 由题意可得m2+n2的最小值为原点到直线l距离的平方，由点到直线的距离公式可得．
解答 解：∵a，b，c为直角三角形中的三边长，c为斜边长，∴c=$\sqrt{{a}^{2}+{b}^{2}}$，
又∵点M（m，n）在直线l：ax+by+2c=0上，
∴m2+n2表示直线l上的点到原点距离的平方，
∴m2+n2的最小值为原点到直线l距离的平方，
由点到直线的距离公式可得d=$\frac{2c}{\sqrt{{a}^{2}+{b}^{2}}}$=2，
∴m2+n2的最小值为d2=4，
故选：C．
点评 本题考查式子的最值，数形结合是解决问题的关键，属基础题．
练习册系列答案
相关题目
5．设f′（x）为函数f（x）的导函数，已知x2f′（x）+xf（x）=lnx，f（1）=$\frac{1}{2}$，则下列结论正确的是（ ）
| A． | f（x）在（0，+∞）上有极大值$\frac{1}{2}$ | B． | f（x）在（0，+∞）上有极小值$\frac{1}{2}$ | ||
| C． | f（x）在（0，+∞）单调递增 | D． | f（x）在（0，+∞）单调递减 |
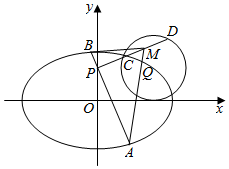已知F1，F2为椭圆${C_1}：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点，F2在以$Q（\sqrt{2}，1）$为圆心，1为半径的圆C2上，且|QF1|+|QF2|=2a．
6．对于直线m，n和平面α，β，能得出α⊥β的一个条件是（ ）
| A． | m⊥n，m∥α，n∥β | B． | m⊥n，α∩β=m，n?α | C． | m∥n，n⊥β，m?α | D． | m∥n，m⊥α，n⊥β |