题目内容

20．在平行六面体ABCD-A1B1C1D1中，化简$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{A{A}_{1}}$=（　　）
A．$\overrightarrow{A{C}_{1}}$B．$\overrightarrow{C{A}_{1}}$C．$\overrightarrow{B{C}_{1}}$D．$\overrightarrow{C{B}_{1}}$

分析 根据题意，画出图形，结合图形，利用空间向量的加法运算，即可得出结论．

解答 解：如图所示，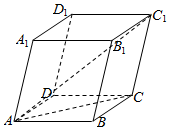

平行六面体ABCD-A1B1C1D1中，
$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{A{A}_{1}}$=（$\overrightarrow{AB}$+$\overrightarrow{AD}$）+$\overrightarrow{C{C}_{1}}$=$\overrightarrow{AC}$+$\overrightarrow{{CC}_{1}}$=$\overrightarrow{{AC}_{1}}$．
故选：A．

点评 本题考查了空间向量的线性运算问题，也考查了数形结合的应用问题，是基础题目．

练习册系列答案
相关题目
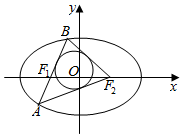10． 如图，设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2，过焦点F1的直线交椭圆于A、B两点，若以△ABF2的内切圆的面积为π，设A（x1，y1）、B（（x2，y2），则|y1-y2|值为$\frac{10}{3}$．
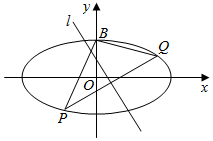11．已知中心在原点O，焦点在x轴上的椭圆的一个顶点为B（0，1），B到焦点的距离为2．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设P，Q是椭圆上异于点B的任意两点，且BP⊥BQ，线段PQ的中垂线l与x轴的交点为（x0，0），求x0的取值范围．
8．已知椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的两焦点分别为F1，F2，过F1的直线与椭圆交于A，B两点，则△ABF2的周长为8．
15．已知p：3x2-4ax+a2＜0（a＞0），q：$\left\{\begin{array}{l}{{x}^{2}-4x+3＜0}\\{{x}^{2}-6x+8≥0}\end{array}\right.$，若p是q的必要条件，求实数a的取值范围．
5．设f′（x）为函数f（x）的导函数，已知x2f′（x）+xf（x）=lnx，f（1）=$\frac{1}{2}$，则下列结论正确的是（　　）
A．f（x）在（0，+∞）上有极大值$\frac{1}{2}$B．f（x）在（0，+∞）上有极小值$\frac{1}{2}$
C．f（x）在（0，+∞）单调递增D．f（x）在（0，+∞）单调递减
12．一个袋中装有四个大小、形状完全相同的小球，小球的编号分别为1，2，3，4．
（Ⅰ）从袋中随机取两个小球，求取出的两个小球的编号之和不小于5的概率；
（Ⅱ）先从袋中随机取一个小球，记此小球的编号为m，将此小球放回袋中，然后再从袋中随机取一个小球，记该小球的编号为n，求n=m+2的概率．
9．已知函数f（x）=2acos2x+2$\sqrt{3}$bsinxcosx，且f（0）=2，f（$\frac{π}{4}$）=$\sqrt{3}$+1．
（1）求f（x）的最大值及单调递减区间；
（2）若α≠β，α，β∈（0，π），且f（α）=f（β），求tan（α+β）的值．
10．已知向量$\overrightarrow{a}$=（sin（2x-$\frac{π}{6}$），cos2$\frac{π}{4}$-cos2x），$\overrightarrow{b}$=（1，-2），函数$f（x）=\vec a•\vec b（x∈R）$
（1）求f（x）的单调递增区间；
（2）f（x）图象可以由y=sinx经过怎样的变换而得到？
（3）求在$x∈（{-\frac{π}{6}，\frac{π}{3}}）$上的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网