题目内容
求函数y=
的值域.
| sec2x+tanx |
| sec2x-tanx |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:函数解析式分子分母利用同角三角函数间基本关系切化弦后,表示出sinxcosx,进而表示出sin2x,根据正弦函数的值域确定出y的值域即可.
解答:
解:y=
=
=
(函数的定义域是x≠
+kπ,k∈Z),
即y-ysinxcosx=1+sinxcosx,
∴sinxcosx=
,即sin2x=
,
∵-1≤sin2x≤1,且sin2x≠0,即-1≤
≤1,且y≠1,
整理得:
且y≠1,即
且y≠1,
解得:
≤y≤3,且y≠1,
则函数的值域为[
,1)∪(1,3].
| sec2x+tanx |
| sec2x-tanx |
| ||||
|
| 1+sinxcosx |
| 1-sinxcosx |
| π |
| 2 |
即y-ysinxcosx=1+sinxcosx,
∴sinxcosx=
| y-1 |
| y+1 |
| 2(y-1) |
| y+1 |
∵-1≤sin2x≤1,且sin2x≠0,即-1≤
| 2(y-1) |
| y+1 |
整理得:
|
|
解得:
| 1 |
| 3 |
则函数的值域为[
| 1 |
| 3 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
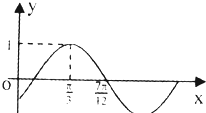 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
函数f(x)=sinx在区间(0,5π)上可找到n(n≥2)个不同数x1,x2,…,xn,使得:
=
=…=
,则自然数n的所有可能取值集合为( )
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(xn) |
| xn |
| A、{2,3} |
| B、{2,3,4} |
| C、{2,3,4,5} |
| D、{3,4,5,6} |