题目内容
等差数列{an}的前n项之和为Sn,若a1=1,且
-
=2,
(1)求an;
(2)求证:
+
+
+…+
>2(
-1).
| S2015 |
| 2015 |
| S2013 |
| 2013 |
(1)求an;
(2)求证:
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2n |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由等差数列{an}的前n项之和为Sn,可知{
}也是等差数列且公差为1,即可求得;
(2)由(1)得
=
=
>
=2(
-
),利用裂项相消法证得结论成立.
| Sn |
| n |
(2)由(1)得
| 1 | ||
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
| 2n |
| 2n-1 |
解答:
解:(1)等差数列{an}的前n项之和为Sn,则{
}也是等差数列且公差为1
所以
=
+(n-1)即Sn=n2
∴an=2n-1
(2)∵
=
=
>
=2(
-
)
所以
+
+
+…+
>2(
-1)
| Sn |
| n |
所以
| Sn |
| n |
| S1 |
| 1 |
∴an=2n-1
(2)∵
| 1 | ||
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
| 2n |
| 2n-1 |
所以
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2n |
点评:本题考查学生对等差数列性质的运用及数列求和方法的运用能力,考查学生放缩法及运算求解能力,属难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
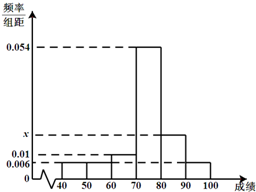 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].