题目内容
设函数y=f(x)的定义域为D,最小值为m,最大值为M,若m∈D且M∈D,则称y=f(x),x∈D为“B函数”若f(x)=
x2-x+
,x∈[1,b]为“B函数”,求实数b的取值范围.
| 1 |
| 2 |
| 3 |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:求出最小值为m=
×12-1+
=1,最大值为M=
b2-b+
,根据题意得出
求解即可.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
|
解答:
解:∵f(x)=
x2-x+
,
∴对称轴为:x=1,
∵x∈[1,b]
∴函数在x∈[1,b]单调递增,
最小值为m=
×12-1+
=1,
最大值为M=
b2-b+
,
∵f(x)为“B函数”,
∴
即1<b≤3.
| 1 |
| 2 |
| 3 |
| 2 |
∴对称轴为:x=1,
∵x∈[1,b]
∴函数在x∈[1,b]单调递增,
最小值为m=
| 1 |
| 2 |
| 3 |
| 2 |
最大值为M=
| 1 |
| 2 |
| 3 |
| 2 |
∵f(x)为“B函数”,
∴
|
即1<b≤3.
点评:本题考查了函数的性质,新概念的题目,关键是列出不等式组,属于中档题.

练习册系列答案
相关题目
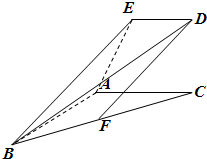 如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.
如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.