Question

在面积为9的正方形ABCD内部随机取一点P，则能使△PAB的面积大于3的概率是（　　）

• A、

  1

  3

• B、

  2

  3

• C、

  1

  9

• D、

  8

  9

Answer 1

考点：几何概型

专题：概率与统计

分析：根据正方形的面积可达正方形的边长，根据△PAB的面积大于3确定P的位置，然后根据几何概型的概率公式进行计算．

解答： 解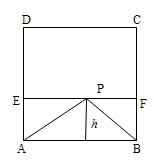：∵正方形ABCD面积为9，∴正方形的边长AB=3．
设△PAB的高为h，
则△PAB的面积等于3时，有

1

2

•AB•h=3，
即

1

2

×3h=3，
∴h=2，即AE=2，
∴要使△PAB的面积大于3，
则h＞2，即顶点P位于矩形CDEF内，
∴根据几何概型的概率公式可知在面积为9的正方形ABCD内部随机取一点P，则能使△PAB的面积大于3的概率为：
S_矩形CDEF：S_矩形ABCD=DE：AE=（3-2）：3=1：3，
故选：A．

点评：本题主要考查几何概型的概率公式的计算，根据三角形的面积确定点P的位置是解决本题的关键．