题目内容
已知向量
=（x，4，1），
=（-2，y，-1），且
∥
，则x= ，y= ．
| a |
| b |
| a |
| b |
考点：向量的数量积判断向量的共线与垂直
专题：空间向量及应用
分析：利用向量平行的性质求解．
解答：
解：∵
=（x，4，1），
=（-2，y，-1），
且
∥
，
∴
=
=
，
解得x=2，y=-4．
故答案为：2，-4．
| a |
| b |
且
| a |
| b |
∴
| x |
| -2 |
| 4 |
| y |
| 1 |
| -1 |
解得x=2，y=-4．
故答案为：2，-4．
点评：本题考查实数值的求法，是基础题，解题时要注意向量平行的性质的合理运用．
练习册系列答案
相关题目
给出以下四个命题：
①在△ABC中，若sinA＞
，则A＞
；
②若1≤x＜2，则（x-1）（x-2）≤0；
③若x=y=0，则x2+y2=0；
④若a•b=a•c（a≠0），则b=c．
则以下判断正确的为（ ）
①在△ABC中，若sinA＞
| ||
| 2 |
| π |
| 4 |
②若1≤x＜2，则（x-1）（x-2）≤0；
③若x=y=0，则x2+y2=0；
④若a•b=a•c（a≠0），则b=c．
则以下判断正确的为（ ）
| A、①的逆否命题为真 |
| B、②的否命题为真 |
| C、③的否命题为假 |
| D、④的逆命题为假 |
把一个长、宽之比为3：2的矩形分别绕其长和宽旋转360°，得到的两个几何体的体积之比为（ ）
| A、1：3 | B、2：3 |
| C、4：9 | D、2：1 |
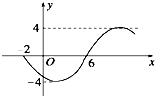函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，x∈R）的部分图象如右图所示，则函数的表达式为（ ）A、f（x）=4sin（
| ||||
B、f（x）=4sin（
| ||||
C、f（x）=4sin（
| ||||
D、f（x）=4sin（
|
设a，b∈R，则“（a-b）a2＞0”是“a＞b”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、既不充分也不必要条件 |
| D、充要条件 |