题目内容
18.已知复数$z=\frac{5}{2i-1}$(i为虚数单位),则z的共轭复数对应的点位于复平面的( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数代数形式的乘除运算化简求出z,进一步得到$\overline{z}$,得到$\overline{z}$的坐标得答案.
解答 解:∵复数$z=\frac{5}{2i-1}=\frac{{5({-2i-1})}}{{({2i-1})({-2i-1})}}=-1-2i$.
∴$\overline z=-1+2i$.
其对应的点为(-1,2),它位于复平面的第二象限.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
13.已知双曲线E$:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,其一渐近线被圆C:(x-1)2+(y-3)2=9所截得的弦长等于4,则E的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ |
3.设正项等差数列{an}的前n项和为Sn,若S2017=4034,则$\frac{1}{a_9}+\frac{9}{{{a_{2009}}}}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | 4 |
10.过抛物线y2=4x的焦点F作直线l交抛物线于A,B两点,若$\frac{1}{|AF|}-\frac{1}{|BF|}$=$\frac{1}{2}$,则直线l的倾斜角θ(0<θ<$\frac{π}{2}$)等于( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
7.若正三棱锥的侧面都是直角三角形,则它的侧棱与底面所成角的余弦值为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
8.如图为某几何体的三视图,则该几何体的内切球的直径为( )
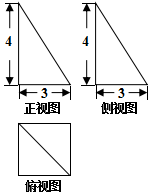

| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |