题目内容
3.如图所示,在正方体ABCD-A1B1C1D1中,下列结论正确的是( )
| A. | 直线A1B与直线AC所成的角是45° | |
| B. | 直线A1B与平面ABCD所成的角是30° | |
| C. | 二面角A1-BC-A的大小是60° | |
| D. | 直线A1B与平面A1B1CD所成的角是30° |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:对于A,连结BC1、A1C1,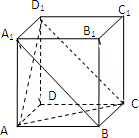
∵在正方体ABCD-A1B1C1D1中,A1A平行且等于C1C,
∴四边形AA1C1C为平行四边形,可得A1C1∥AC,
因此∠BA1C1(或其补角)是异面直线A1B与AC所成的角,
设正方体的棱长为a,则△A1B1C中A1B=BC1=C1A1=$\sqrt{2}$a,
∴△A1B1C是等边三角形,可得∠BA1C1=60°,
即异面直线A1B与AC所成的角等于60°.即A不正确;
直线A1B与平面ABCD所成的角是∠A1BA=45°,即B不正确;
二面角A1-BC-A的平面角是∠A1BA=45°,即C不正确;
因为BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,所以∠BA1O为A1B与平面A1B1CD所成的角.设正方体的棱长为a
在RT△A1BO中,A1B=$\sqrt{2}$a,BO=$\frac{\sqrt{2}}{2}$a,所以BO=$\frac{1}{2}$A1B,∠BA1O=30°,
即直线A1B和平面A1B1CD所成的角为30°,即D正确.
故选D.
点评 本题在正方体中求异面直线所成角和直线与平面所成角的大小,着重考查了正方体的性质、空间角的定义及其求法等知识,属于中档题.

练习册系列答案
相关题目
13.已知双曲线E$:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,其一渐近线被圆C:(x-1)2+(y-3)2=9所截得的弦长等于4,则E的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ |
14.设集合A={1,2,3},B={2,4,6,8},则A∩B=( )
| A. | {2} | B. | {2,3} | C. | {1,2,3,4,6,8} | D. | {1,3} |
11.若复数z满足:z+2i=$\frac{3-{i}^{3}}{1+i}$(i为虚数单位),则|z|等于( )
| A. | $\sqrt{13}$ | B. | 3 | C. | 5 | D. | $\sqrt{5}$ |
8.如图为某几何体的三视图,则该几何体的内切球的直径为( )
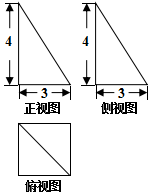

| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
12.下列哪种工作不能使用抽样方法进行( )
| A. | 测定一批炮弹的射程 | |
| B. | 测定海洋水域的某种微生物的含量 | |
| C. | 高考结束后,国家高考命题中心计算数学试卷中每个题目的难度 | |
| D. | 检测某学校全体高二学生的身高和体重的情况 |
13.“${(\frac{1}{3})^x}<1$”是“$\frac{1}{x}>1$”的( )
| A. | 必要且不充分条件 | B. | 充分且不必要条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |