题目内容
对于函数f(x)=xm(1-x)n(m∈N*,n∈N*),下列命题正确的有 .(写出所有正确命题的序号)
①f(x)值域为R;
②对任意不全为奇数的m,n.函数f(x)的图象与x轴相切;
③函数f(x)一定存在极值;
④存在m,n,使f(x)为奇函数;
⑤当x?[0,1]时,f(x)≤
.
①f(x)值域为R;
②对任意不全为奇数的m,n.函数f(x)的图象与x轴相切;
③函数f(x)一定存在极值;
④存在m,n,使f(x)为奇函数;
⑤当x?[0,1]时,f(x)≤
| 1 |
| 4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:取m,n为偶数判断①;分别取m,n为偶数判断②;由f(0)=f(1)=0,且f(x)在区间(0,1)内连续判断③;举反例判断④;由函数的单调性及m=n=1时f(x)=x(1-x)≤
判断⑤.
| 1 |
| 4 |
解答:
解:对于①,当m,n均为偶数时,f(x)≥0,故①错误;
对于②,当m为偶数时,f(x)的图象与x轴相切于(0,0),当n为偶数时,f(x)的图象与x轴相切于(1,0),故②正确;
对于③,∵f(0)=f(1)=0,且f(x)在区间(0,1)内连续,
∴f(x)在区间(0,1)内不单调,故有极值点,故③正确;
对于④,∵f(1)=0且f(-1)≠0,故④错误;
对于⑤,当x∈[0,1]时,随着m,n的增大f(x)的函数值变小,当m=n=1时,f(x)=x(1-x)≤
,故⑤正确.
∴正确的命题是②③⑤.
故答案为:②③⑤.
对于②,当m为偶数时,f(x)的图象与x轴相切于(0,0),当n为偶数时,f(x)的图象与x轴相切于(1,0),故②正确;
对于③,∵f(0)=f(1)=0,且f(x)在区间(0,1)内连续,
∴f(x)在区间(0,1)内不单调,故有极值点,故③正确;
对于④,∵f(1)=0且f(-1)≠0,故④错误;
对于⑤,当x∈[0,1]时,随着m,n的增大f(x)的函数值变小,当m=n=1时,f(x)=x(1-x)≤
| 1 |
| 4 |
∴正确的命题是②③⑤.
故答案为:②③⑤.
点评:本题考查了命题的真假判断与应用,考查了特值验证法及举反例法判断命题的真假,考查了由函数的单调性求函数的值域,是中档题.

练习册系列答案
相关题目
已知平面直角坐标系xOy内直线l的参数方程为
(t为参数),以Ox为极轴建立极坐标系(取相同的长度单位),圆C的极坐标方程为ρ=2
sin(θ+
),则直线l与圆C的公共点的个数为 .
|
| 2 |
| π |
| 4 |
在△ABC中,设命题p:
=
=
,命题q:△ABC是等边三角形,那么命题p是命题q的( )
| a |
| sinC |
| b |
| sinA |
| c |
| sinB |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在复平面内与复数z=
所对应的点关于实轴对称的点为A,则A对应的复数为( )
| 2i |
| 1+i |
| A、1+i | B、1-i |
| C、-1-i | D、-1+i |
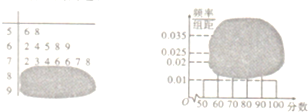 某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题;
某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题; 如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,已知⊙O的半径为3,PA=2,则OE=
如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,已知⊙O的半径为3,PA=2,则OE=