题目内容
6．将一枚硬币先后抛掷两次，恰好出现一次正面的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{3}$ |
分析 将一枚硬币先后抛掷两次，利用列举法求出基本事件个数和恰好出现一次正面的情况的种数，由此能求出将一枚硬币先后抛掷两次，恰好出现一次正面的概率．
解答 解：将一枚硬币先后抛掷两次，
基本事件有：{正正}，{正反}，{反正}，{反反}，共有4 个，
恰好出现一次正面的情况有两种，
∴将一枚硬币先后抛掷两次，恰好出现一次正面的概率是p=$\frac{2}{4}=\frac{1}{2}$．
故选：B．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．
练习册系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
16．函数f（x）=2cos（$\frac{x}{2}+\frac{π}{4}$）（x∈R）的最小正周期为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
17．函数f（x）=$\frac{1}{2-x}$+$\sqrt{9-{x}^{2}}$的定义域为（ ）
| A． | {x|x≠2} | B． | {x|x＜-3或x＞3} | C． | {x|-3≤x≤3} | D． | {x|-3≤x≤3且≠2} |
14．已知集合M={1，2，3}，N={1，3，4}，则M∩N=（ ）
| A． | {1，3} | B． | {1，2，3，4} | C． | {2，4} | D． | {1，3，4} |
11．已知α，β，γ是空间三个不重合的平面，m，n是空间两条不重合的直线，则下列命题为真命题的是（ ）
| A． | 若α⊥β，β⊥γ，则α∥γ | B． | 若α⊥β，m∥β，则m⊥α | C． | 若m⊥α，n⊥α，则m∥n | D． | 若m∥α，n∥α，则m∥n |
18．函数 y=sin$\frac{x}{2}$，x∈R的最小正周期是（ ）
| A． | 4π | B． | 2π | C． | π | D． | $\frac{π}{2}$ |
15．
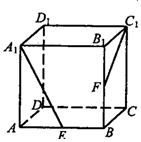如图，ABCD-A1B1C1D1是正方体，E、F分别是AB、BB1的中点，则异面直线A1E与C1F所成角的余弦值为（ ）
如图，ABCD-A1B1C1D1是正方体，E、F分别是AB、BB1的中点，则异面直线A1E与C1F所成角的余弦值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{5}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
18．设集合A={x|x2＜4}，B={1，2，3}，则A∩B=（ ）
| A． | {1，2，3} | B． | {1，2} | C． | {1} | D． | {2} |