题目内容
11.已知α,β,γ是空间三个不重合的平面,m,n是空间两条不重合的直线,则下列命题为真命题的是( )| A. | 若α⊥β,β⊥γ,则α∥γ | B. | 若α⊥β,m∥β,则m⊥α | C. | 若m⊥α,n⊥α,则m∥n | D. | 若m∥α,n∥α,则m∥n |
分析 由垂直于同一平面的两平面的位置关系判断A;由空间中的线面关系判断B;由线面垂直的性质判断C;由平行于同一平面的两直线的位置关系判断D.
解答 解:由α⊥β,β⊥γ,得α∥γ或α与γ相交,故A错误;
由α⊥β,m∥β,得m∥α或m?α或m与α相交,故B错误;
由m⊥α,n⊥α,得m∥n,故C正确;
由m∥α,n∥α,得m∥n或m与n相交或m与n异面,故D错误.
故选:C.
点评 本题考查命题的真假判断与应用,考查了空间中的线面关系,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为10,一条渐近线为y=$\frac{1}{2}$x,则该双曲线的方程为( )
| A. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}$=1 | C. | $\frac{{x}^{2}}{80}-\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{80}$=1 |
2.若直线l1:(m-2)x-y-1=0,与直线l2:3x-my=0互相平行,则m的值等于( )
| A. | 0或-1或3 | B. | 0或3 | C. | 0或-1 | D. | -1或3 |
19.执行如图所示的程序框图,当输入x为16时,输出的y=( )
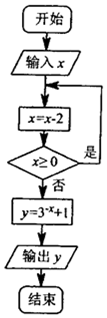

| A. | 28 | B. | 10 | C. | 4 | D. | 2 |
6.将一枚硬币先后抛掷两次,恰好出现一次正面的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
3.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的离心率等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
20.函数f(x)=$\frac{1}{2}$x2-lnx,在(1,$\frac{1}{2}$)处的切线斜率为( )
| A. | 1 | B. | 2 | C. | 0 | D. | $\frac{1}{2}$ |