题目内容
15．
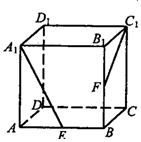如图，ABCD-A1B1C1D1是正方体，E、F分别是AB、BB1的中点，则异面直线A1E与C1F所成角的余弦值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{5}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
分析 首先找到异面直线的夹角的平面角，然后利用勾股定理及余弦定理求出相应的值．
解答 
解：在正方体ABCD-A1B1C1D1中，E、F是AB、BB1的中点，设AB=4
取A1B1的中点H，HB1的中点G，连结GF，GC1，
GF、FC1所成的角即为A1E与C1F所成的角．
利用勾股定理得：GF=$\sqrt{5}$，C1F=2$\sqrt{5}$，GC1=$\sqrt{17}$，
在△CFG中，利用余弦定理
cos∠GFC1=$\frac{5+20-17}{2•\sqrt{5}•2\sqrt{5}}$=$\frac{2}{5}$．
故选：B
点评 本题考查的知识点：异面直线的夹角，勾股定理的应用，余弦定理的应用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
5．若sinα=$\frac{4}{5}$，且α为锐角，则tanα的值等于（ ）
| A． | $\frac{4}{3}$ | B． | -$\frac{3}{4}$ | C． | $\frac{3}{4}$ | D． | -$\frac{4}{3}$ |
6．将一枚硬币先后抛掷两次，恰好出现一次正面的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{3}$ |
3．椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的离心率等于（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
10．已知sinα=$\frac{1}{4}$，则cos2α的值为（ ）
| A． | -$\frac{7}{8}$ | B． | $\frac{7}{8}$ | C． | $\frac{1}{2}$ | D． | $\frac{15}{16}$ |
20．函数f（x）=$\frac{1}{2}$x2-lnx，在（1，$\frac{1}{2}$）处的切线斜率为（ ）
| A． | 1 | B． | 2 | C． | 0 | D． | $\frac{1}{2}$ |
7．若向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），则2$\overrightarrow{a}$-$\overrightarrow{b}$的坐标为（ ）
| A． | （1，5） | B． | （1，1） | C． | （5，4） | D． | （3，5） |
