题目内容
12.命题“若x2∈R,则x2+1>1”的逆否命题是若x2+1≤1,则x∉R;并判定原命题是真命题还是假命题?假命题.分析 否定命题的条件作结论,否定命题的结论作条件,即可写出命题的逆否命题.举x=0可以判断真假
解答 解:由命题与逆否命题的关系可知:命题“若x2∈R,则x2+1>1”的逆否命题是:若x2+1≤1,则 x∉R,
当x=0时,时命题不成立,
原命题为假命题,
故答案为:若x2+1≤1,则 x∉R,假命题
点评 本题考查四种命题的逆否关系,搞清楚关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.函数f(x)=$\frac{ln(4-x)}{x-2}$的定义域是( )
| A. | (-∞,4) | B. | (2,4) | C. | (0,2)∪(2,4) | D. | (-∞,2)∪(2,4) |
3.已知lg(x+y)=lgx+lgy,则x+y的取值范围是( )
| A. | (0,1] | B. | [2,+∞) | C. | (0,4] | D. | [4,+∞) |
7.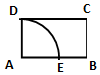 如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )
 如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )| A. | $\frac{\sqrt{3}π}{12}$ | B. | $\frac{12-\sqrt{3}π}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
17.函数$y=sin(ωx+\frac{π}{6})(ω>0)$的图象与x轴正半轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,若要得到函数g(x)=sinωx的图象,只要将f(x)的图象( )个单位.
| A. | 向左平移$\frac{π}{12}$ | B. | 向右平移$\frac{π}{12}$ | C. | 向左平移$\frac{π}{6}$ | D. | 向右平移$\frac{π}{6}$ |
4.执行如图的程序框图,则输出的n是( )
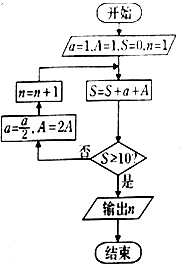

| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
2.命题“?x>0,lnx>0”的否定是( )
| A. | ?x>0,lnx>0 | B. | ?x>0,lnx>0 | C. | ?x>0,lnx≥0 | D. | ?x>0,lnx≤0 |