题目内容
讨论函数f(x)=(
)|x|的定义域、值域、奇偶性,作出它的图象,并根据图象求出函数的单调区间.
| 1 |
| 2 |
考点:指数函数的图像变换,指数函数的定义、解析式、定义域和值域
专题:函数的性质及应用
分析:当x≥0时,函数为y=(
)x;当x<0时,函数为y=(
)-x=2x,利用指数函数的图象可得结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:当x≥0时,函数为y=(
)x;
当x<0时,函数为y=(2)-x=2x,其图象由y=(
)x(x≥0)和y=2x(x<0)的图象合并而成.
而y=(
)x(x≥0)和y=2x(x<0)的图象关于y轴对称,所以原函数图象关于y轴对称.图象如图
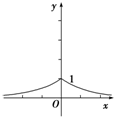
由图象可知,定义域为R,值域是(0,1],为偶函数,递增区间是(-∞,0],递减区间是[0,+∞).
| 1 |
| 2 |
当x<0时,函数为y=(2)-x=2x,其图象由y=(
| 1 |
| 2 |
而y=(
| 1 |
| 2 |

由图象可知,定义域为R,值域是(0,1],为偶函数,递增区间是(-∞,0],递减区间是[0,+∞).
点评:本题考查函数图象的画法,考查数形结合的数学思想,正确作图是关键.

练习册系列答案
相关题目
 函数y=
函数y=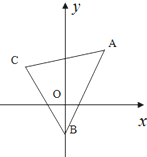 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3).求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3).求: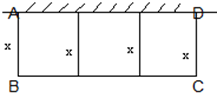 有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求:
有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求: