题目内容
若数列{an}与{bn}满足bn+1an+bnan+1=(-1)n+1,bn=
,n∈N+,且a1=2,设数列{an}的前n项和为Sn,则S63= .
| 3+(-1)n-1 |
| 2 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:由已知条件推导出bn=
,an=
,由此能求出S63.
|
|
解答:
解:∵bn=
,
∴bn=
,
∵bn+1an+bnan+1=(-1)n+1,
∴当n为奇数时,an+2an+1=0,
当n为偶数时,2an+an+1=2,
∵a1=2,
∴an=
,
∴S63=
-
=560
故答案为:560.
| 3+(-1)n-1 |
| 2 |
∴bn=
|
∵bn+1an+bnan+1=(-1)n+1,
∴当n为奇数时,an+2an+1=0,
当n为偶数时,2an+an+1=2,
∵a1=2,
∴an=
|
∴S63=
| (2+64)×32 |
| 2 |
| (1+31)×31 |
| 2 |
故答案为:560.
点评:本题考查数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力以及分类讨论思想.

练习册系列答案
相关题目
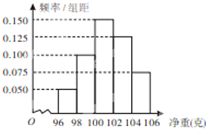 给出下列五个命题:
给出下列五个命题: 下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为
下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为