题目内容
已知集合A={x|x2-mx+m2-7=0},B={x|x2-3x+2=0},C={x|x2+4x-5=0},若A∩B≠∅且A∩C=∅,求实数m的值.
考点:集合的包含关系判断及应用
专题:集合
分析:由题意,可先化简两个集合,再由A∩B≠∅且A∩C=∅判断出2∈A,代入解出m的值,再验证即可得出答案
解答:
解:由题意,B={x|x2-3x+2=0}={1,2},C={x|x2+4x-5=0}={-5,1},
又A∩B≠∅且A∩C=∅,可得2∈A,
∴4-2m+m2-7=0,解得m=3或-1.
当m=3时,可解得A={1,2},这与A∩C=∅矛盾,故舍.
m=-1为所求.
又A∩B≠∅且A∩C=∅,可得2∈A,
∴4-2m+m2-7=0,解得m=3或-1.
当m=3时,可解得A={1,2},这与A∩C=∅矛盾,故舍.
m=-1为所求.
点评:本题考查集合的包含关系及应用,根据题设条件得出2∈A是解答的关键,本题是一个易错题,易因为忘记验证导致未能排除m=3.

练习册系列答案
相关题目
直线y-1=k(x-3)被圆(x-2)2+(y-2)2=4所截得的最短弦长等于( )
A、
| ||
B、2
| ||
C、2
| ||
D、
|
在一次学习方法交流会上,需要交流示范学校的5篇论文和非示范学校的3篇论文,交流顺序可以是任意的,则最先和最后交流的论文不能来自同类学校的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
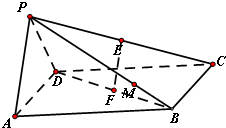 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点. 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.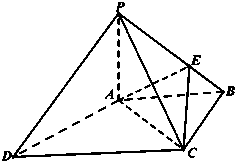 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点. 四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为
四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为