题目内容
设数列{an}满足an+1=an2-nan+1,n=1,2,3…当a1≥3时,证明对所有的n∈正整数都有
+
+…+
<
.
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:用数学归纳法证明an≥n+2.从而得到
≤
•
,k≥2,由此利用放缩法能证明
+
+…+
<
.
| 1 |
| 1+an |
| 1 |
| 1+a1 |
| 1 |
| 2k-1 |
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| 1 |
| 2 |
解答:
证明:用数学归纳法证明an≥n+2.
①当n=1时,a1≥3=1+2,不等式成立;
②假设当n=k时不等式成立,即ak≥k+2,
那么,ak+1=ak(ak-k)+1≥(k+2)(k+2-k)+1≥k+3,
也就是说,当n=k+1时,ak+1≥(k+1)+2,
根据①和②,对于所有n≥1,有an≥n+2.
∵an+1=an2-nan+1=an(an-n)+1,an≥n+2,
∴对k≥2,有ak=ak-1(ak-1-k+1)
≥ak-1(k-1+2-k+1)+1=2ak-1+1,
∴ak≥2k-1a1+2k-2+…+2+1=2k-1(a1+1)-1,
于是
≤
•
,k≥2,
∴
≤
+
•
=
≤
≤
=
.
∴
+
+…+
<
.
①当n=1时,a1≥3=1+2,不等式成立;
②假设当n=k时不等式成立,即ak≥k+2,
那么,ak+1=ak(ak-k)+1≥(k+2)(k+2-k)+1≥k+3,
也就是说,当n=k+1时,ak+1≥(k+1)+2,
根据①和②,对于所有n≥1,有an≥n+2.
∵an+1=an2-nan+1=an(an-n)+1,an≥n+2,
∴对k≥2,有ak=ak-1(ak-1-k+1)
≥ak-1(k-1+2-k+1)+1=2ak-1+1,
∴ak≥2k-1a1+2k-2+…+2+1=2k-1(a1+1)-1,
于是
| 1 |
| 1+an |
| 1 |
| 1+a1 |
| 1 |
| 2k-1 |
∴
| n |
 |
| k=1 |
| 1 |
| 1+ak |
| 1 |
| 1+a1 |
| 1 |
| 1+a1 |
| n |
 |
| k=2 |
| 1 |
| 2k-1 |
=
| 1 |
| 1+a1 |
| n |
 |
| k=1 |
| 1 |
| 2k-1 |
| 2 |
| 1+a1 |
| 2 |
| 1+3 |
| 1 |
| 2 |
∴
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| 1 |
| 2 |
点评:本题考查不等式的证明,是中档题,解题时要认真审题,注意数学归纳法和放缩法的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
在独立性检验中,若随机变量k2≥6.635,则( )
| A、x与y有关系,犯错的概率不超过1% |
| B、x与y有关系,犯错的概率超过1% |
| C、x与y没有关系,犯错的概率不超过1% |
| D、x与y没有关系,犯错的概率超过1% |
设P和Q是两个集合,定义集合P-Q={x|x∈P且x∉Q},如果P={x|x2-2x<0},Q={x|1≤x<3},那么P-Q=( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|1≤x<2} |
| D、{x|2≤x<3} |
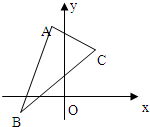 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).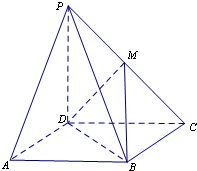 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.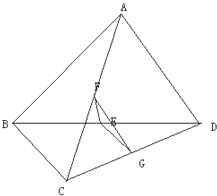
 在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.
在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.