题目内容
已知函数f（x）=ax-x-a（a＞0，a≠1），那么函数f（x）的零点个数是（ ）
| A、0个 | B、1个 |
| C、2个 | D、至少1个 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由f（x）=0，将函数转化为ax=x+a，将方程转化为函数，利用数形结合即可得到结论．
解答：
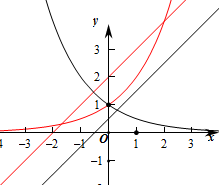解：由f（x）=ax-x-a=0，则ax=x+a，设y=ax，y=x+a，
若a＞1，作出两个函数的图象，则此时两个图象有两个交点，即函数f（x）的零点有2个，（红线部分）
若0＜a＜1，作出两个函数的图象，则此时两个图象有1个交点，即函数f（x）的零点有1个，
综上函数f（x）的零点个数是1个或2个，
故选：D．
解：由f（x）=ax-x-a=0，则ax=x+a，设y=ax，y=x+a，若a＞1，作出两个函数的图象，则此时两个图象有两个交点，即函数f（x）的零点有2个，（红线部分）
若0＜a＜1，作出两个函数的图象，则此时两个图象有1个交点，即函数f（x）的零点有1个，
综上函数f（x）的零点个数是1个或2个，
故选：D．
点评：本题主要考查函数零点个数的判断，利用方程和函数之间的关系，转化为两个图象的交点个数问题，利用数形结合是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
双曲线
-
=1的焦点到渐近线的距离为（ ）
| x2 |
| 4 |
| y2 |
| 12 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、2
|
下列各选项中，与sin2008°最接近的数是（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
定义在R上的偶函数f（x）的部分图象如图所示，则区间（-2，0）上下列函数的图象与f（x）的单调性相同的个数是（ ）（Ⅰ）y=x2+1
（Ⅱ）y=|x|+1
（Ⅲ）y=
|
（Ⅳ）y=sinx．
| A、0 | B、1 | C、2 | D、3 |
给定两个向量
=（3，4），
=（x，1），若
⊥
，则x的值等于（ ）
| a |
| b |
| a |
| b |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
不等式|x+3|-|x-1|≤a2-3a，对任意实数x恒成立，则实数a的取值范围为（ ）
| A、（-∞，-2]∪[5，+∞） |
| B、[-1，4] |
| C、[-2，5] |
| D、（-∞，-1]∪[4，+∞） |
设函数f（x）、g（x）分别是定义在R上的奇函数和偶函数，f′（x），g′（x）分别是f（x），g（x）的导函数，当x＜0时，f′（x）•g（x）+f（x）•g′（x）＞0且g（-3）=0，则f（x）•g（x）＜0的解集是（ ）
| A、（-3，0）∪（0，3） |
| B、（-3，0）∪（3，+∞） |
| C、（-∞，-3）∪（3，+∞） |
| D、（-∞，-3）∪（0，3） |
设a＞0，b＞0，
是a与b的等差中项ax=by=3，则
+
的最大值等于（ ）
| 3 |
| 1 |
| x |
| 1 |
| y |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
