题目内容
如图,C、D是以AB为直径的圆上两点,AB=2AD=2
,AC=BC,F是AB上一点,且AF=
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=
.
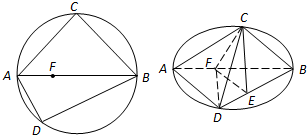
(1)求证:AD⊥平面BCE;
(2)求三棱锥A-CFD的体积.
(3)异面直线AC与BD所成角的余弦值.
| 3 |
| 1 |
| 3 |
| 2 |

(1)求证:AD⊥平面BCE;
(2)求三棱锥A-CFD的体积.
(3)异面直线AC与BD所成角的余弦值.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)根据直径所对的圆周角为直角,得到AD⊥BD,结合CE⊥平面ADB得AD⊥CE,所以AD⊥平面BCE.
(2)由已知条件求出F到AD的距离等于E到AD的距离,由VA-CFD=VC-AFD,利用等积法能求出三棱锥A-CFD的体积.
(3)以E为原点,EF为x轴,ED为y轴,EC为z轴,建立空间直角坐标系,利用向量法能求出异面直线AC与BD所成角的余弦值.
(2)由已知条件求出F到AD的距离等于E到AD的距离,由VA-CFD=VC-AFD,利用等积法能求出三棱锥A-CFD的体积.
(3)以E为原点,EF为x轴,ED为y轴,EC为z轴,建立空间直角坐标系,利用向量法能求出异面直线AC与BD所成角的余弦值.
解答:
(1)证明:依题意:AD⊥BD.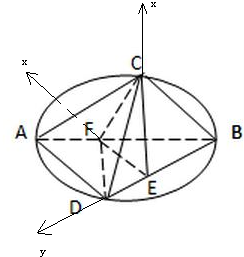
∵CE⊥平面ABD.∴CE⊥AD.
∵BD∩CE=E,∴AD⊥平面BCE.
(2)解:Rt△BCE中,CE=
,BC=
,
∴BE=2,Rt△ABD中,AB=2
,AD=
,∴BD=3.
∴
=
=
,
∴AD∥EF,AD⊥ED,且ED=BD-BE=1,
∴F到AD的距离等于E到AD的距离,为1.
∴S△FAD=
×
×1=
,
∵CE⊥平面ABD,
∴VA-CFD=VC-AFD=
×S△FAD×CE=
×
×
=
.
(3)解:以E为原点,EF为x轴,ED为y轴,EC为z轴,
建立空间直角坐标系,
则A(
,
,0),C(0,0,
),
D(
,0,0),B(-
,0,0),
=(-
,-
,
),
=(-3,0,0),
cos<
,
>=
=
.
∴异面直线AC与BD所成角的余弦值为
.

∵CE⊥平面ABD.∴CE⊥AD.
∵BD∩CE=E,∴AD⊥平面BCE.
(2)解:Rt△BCE中,CE=
| 2 |
| 6 |
∴BE=2,Rt△ABD中,AB=2
| 3 |
| 3 |
∴
| BF |
| BA |
| BE |
| BD |
| 2 |
| 3 |
∴AD∥EF,AD⊥ED,且ED=BD-BE=1,
∴F到AD的距离等于E到AD的距离,为1.
∴S△FAD=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∵CE⊥平面ABD,
∴VA-CFD=VC-AFD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 6 |
(3)解:以E为原点,EF为x轴,ED为y轴,EC为z轴,
建立空间直角坐标系,
则A(
| 3 |
| 3 |
| 2 |
| 2 |
D(
| 3 |
| 2 |
| 3 |
| 2 |
| AC |
| 3 |
| 3 |
| 2 |
| 2 |
| BD |
cos<
| AC |
| BD |
3
| ||||
3×
|
2
| ||
| 29 |
∴异面直线AC与BD所成角的余弦值为
2
| ||
| 29 |
点评:本题将圆沿直径翻折,求证面面垂直和线面平行,着重考查了空间线面平行的判定、线面垂直的性质和面面垂直的判定等知识,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=ax-x-a(a>0,a≠1),那么函数f(x)的零点个数是( )
| A、0个 | B、1个 |
| C、2个 | D、至少1个 |
执行右边的程序框图,若p=0.8,则输出的S,n分别为( )


| A、0.875,3 |
| B、0.875,4 |
| C、0.9375,4 |
| D、0.9375,5 |
 现有一个寻宝游戏,规则如下:在起点P处有A、B、C三条封闭的单向线路,走完这三条线路所花费的时间分别为10分钟、20分钟、30分钟,游戏主办方将宝物放置在B线路上(参赛方并不知晓),开始寻宝时参赛方在起点处随机选择路线顺序,若没有寻到宝物,重新回到起点后,再从没有走过的线路中随机选择路线继续寻宝,直到寻到宝物并将其带回至P处,期间所花费的时间记为X.
现有一个寻宝游戏,规则如下:在起点P处有A、B、C三条封闭的单向线路,走完这三条线路所花费的时间分别为10分钟、20分钟、30分钟,游戏主办方将宝物放置在B线路上(参赛方并不知晓),开始寻宝时参赛方在起点处随机选择路线顺序,若没有寻到宝物,重新回到起点后,再从没有走过的线路中随机选择路线继续寻宝,直到寻到宝物并将其带回至P处,期间所花费的时间记为X.