题目内容
12.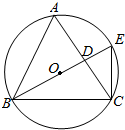 如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.
如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.(1)证明:$\frac{AB}{BD}$=$\frac{BE}{BC}$;
(2)若△ABC的面积S1=$\frac{\sqrt{3}}{4}$BD•BE,证明:$\frac{S}{{S}_{1}}$=$\frac{4\sqrt{3}π}{9}$.
分析 (1)推导出∠ABD=∠CBE,∠BA=∠BEC,从而△ABD∽△EBC,由此能证明$\frac{AB}{BD}$=$\frac{BE}{BC}$.
(2)推导出AB=AC=BC,半径R=OB=2OD=2DE,由此能证明$\frac{S}{{S}_{1}}$=$\frac{4\sqrt{3}π}{9}$.
解答 证明:(1)∵$\widehat{AE}$=$\widehat{CE}$,∴∠ABD=∠CBE,
∵∠BA=∠BEC,∴△ABD∽△EBC,
∴$\frac{AB}{BE}=\frac{BD}{BC}$,∴$\frac{AB}{BD}$=$\frac{BE}{BC}$.
(2)∵点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S,
∴AB=AC=BC,圆心O是等边△ABC的重心,且O在BE上,半径R=OB=2OD=2DE,
∵S1=$\frac{\sqrt{3}}{4}$BD•BE,∴S1=$\frac{\sqrt{3}}{4}•(r+\frac{1}{2}r)(r+r)$=$\frac{3\sqrt{3}}{4}{r}^{2}$,
圆O的面积为S=πr2,
∴$\frac{S}{{S}_{1}}$=$\frac{π{r}^{2}}{\frac{3\sqrt{3}}{4}{r}^{2}}$=$\frac{4\sqrt{3}π}{9}$.
点评 本题考查两组线段比值相等的证明,考查圆的面积与三角形面积比值的证明,是中档题,解题时要认真审题,注意圆的简单性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知双曲线$\frac{x^2}{4}$-$\frac{y^2}{b^2}$=1(b>0)的离心率等于$\frac{\sqrt{3}}{3}$b,则该双曲线的焦距为( )
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 6 | D. | 8 |
4.在8件同类产品中,有5件正品,3件次品,从中任意抽取4件,下列事件中的必然事件是( )
| A. | 4件都是正品 | B. | 至少有一件次品 | C. | 4件都是次品 | D. | 至少有一件正品 |
19.点A(1,1)在直线l:mx+ny=1上,则mn的最大值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
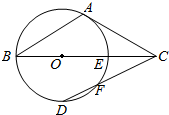 如图,C点在圆O直径BE的延长线上,CA切圆O于A点,CE=OE,CD交⊙O于点D、F.
如图,C点在圆O直径BE的延长线上,CA切圆O于A点,CE=OE,CD交⊙O于点D、F.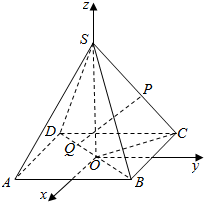 在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.
在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.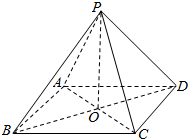 已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.
已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.